就 网上 一视频 一评论 一网友 之所问 之解析 飨以诸君

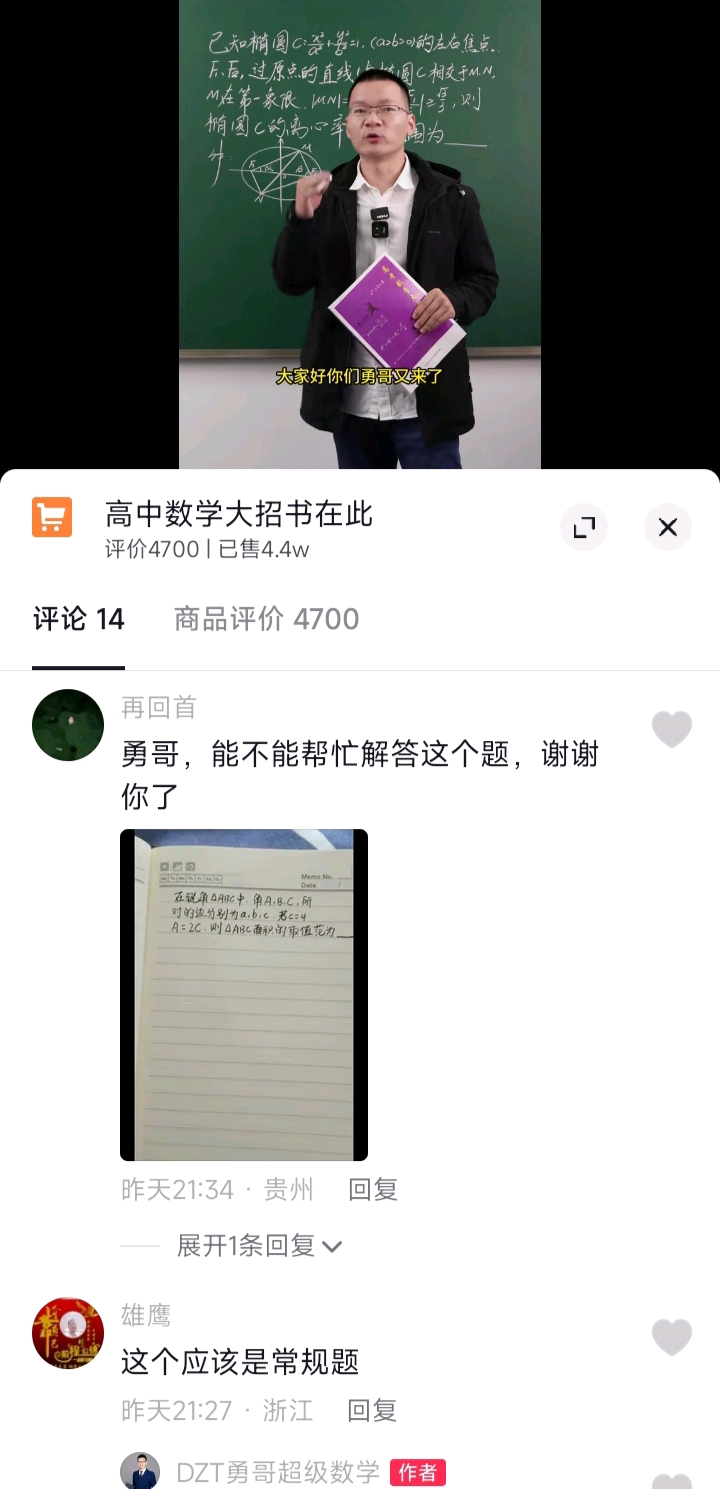
有

a/sin2C=4/sinC

即

a

=

4sin2C/sinC

=

8cosC

且

sinB

=

sin(π-A-C)

=

sin(π-3C)

=

sin3C

即

S△ABC

=

1/2acsinB

=

16sin3CcosC

且

A，B，C∈（0，π/2）

即

2C，π-3C，C∈（0，π/2）

即

C∈(π/6，π/4)

即

tan²C∈(1/3，1)

设

3cos3CcosC-sin3CsinC=0

有

tan3CtanC=3

即

tanC(tan2C+tanC)/(1-tan2CtanC)=3

即

(3tan²C-tan^4C)/(1-3tan²C)=3

即

tan^4C-12tan²C+3=0

即

tan²C=6-√33

且

289＜297

即

17＜3√33

即

17/3＜√33

即

6-√33＜1/3

即

tan²C∉(1/3，1)

设

C=π/6

有

16sin3CcosC=8√3

设

C=π/4

有

16sin3CcosC=8

综

S△ABC∈（8，8√3）

ps.

未见答案

仅供参考