Calculus(88)——Cauchy-Goursat Theorem

2023-06-26 23:34 作者:Mark-McCutcheon 0人读过 | 我要投稿

To accustom myself to the imminent mathematics course which will be taught in English totally in the university and practice my English writing,I will write latter articles in English.However,because I'm only a prospective college student,maybe there will be lots of mistakes and error concerning grammar,words and sentences,please don't mind.

In this article,we will study the Cauchy Integral theorem deeperly.

(the original edition of Cauchy theorem)

If a function $f(z)$ is analytic on a single-connective domain and there is a curve $C$ which is a piecewisely smooth simple closed curve and is included entirely by the domain,then we have

$%5C%5C%5Cint_%7BC%7Df(z)%20%5C%20dz%3D0$

Virtually,because a curve which is not simple can be divided into several simple curves by disconnecting its junctions,we can cancel the condition "simple" in the theorem.

From another aspect,since we said that a function is analytic on a closed domain means it is analytic on a domain including this closed domain,we can change the theorem into a version as follows:

(a better edition)

If a function $f(z)$ is analytic on a closed domain

$%5C%5C%5Cbar%7BD%7D%3DD%5Ccup%20%20C$

and $C$ is a piecewisely smooth simple closed curve,then we have

$%5C%5C%5Cint_%7BC%7Df(z)%20%5C%20dz%3D0$

Actually we have a ultimate version of the theorem concerning the single-connective domain.

(ultimate edition)

There is a curve $C$ which is piecewisely smooth and simple closed with interior $D$ .Function $f(z)$ is analytic on $D$ and is continuous on

$%5C%5C%5Cbar%7BD%7D%3DD%5Ccup%20%20C$

then we have

$%5C%5C%5Cint_%7BC%7Df(z)%20%5C%20dz%3D0$

Theorem on complex-connected domain

Consider

$%5C%5CC_0%2CC_1%2C%E2%80%A6%2CC_n$

which are piecewisely smooth simple closed curves.Among them,

$%5C%5CC_1%2CC_2%2C%E2%80%A6%2CC_n$

are all included in the exterior of each other,but them are also all included in the interior of curve $C_0$ .Then we say that the point set in $C_0$ and simultaneously out of

$%5C%5CC_1%2CC_2%2C%E2%80%A6%2CC_n$

is a complex-connected domain $D$ with

$%5C%5CC_0%2CC_1%2C%E2%80%A6%2CC_n$

as its boundary:

$%5C%5CC%3DC_0%2BC_1%5E-%2BC_2%5E-%2B%E2%80%A6%2BC_n%5E-$

If an observer move along the boundary orientating its positive direction,points of the point set will always be on the observer's left.Such as

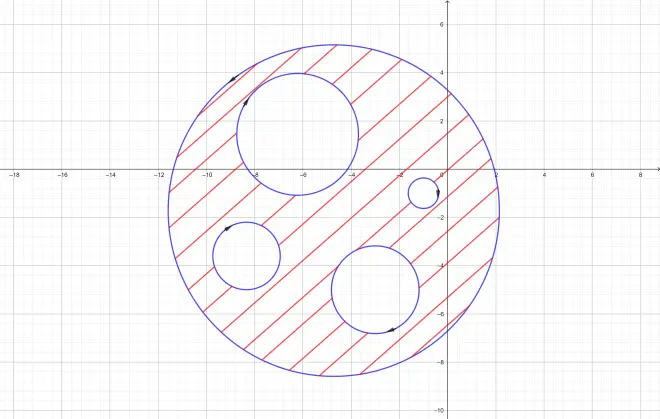
Under this circumstance,if function $f(z)$ is analytic on $D$ and is continuous on

$%5C%5C%5Cbar%7BD%7D%3DD%5Ccup%20%20C$

then we have

$%5C%5C%5Cint_%7BC%7Df(z)%20%5C%20dz%3D0$

$%5C%5C%5Cint_%7BC_0%7Df(z)%20%5C%20dz%2B%5Cint_%7BC_1%5E-%7Df(z)%20%5C%20dz%2B%E2%80%A6%2B%5Cint_%7BC_n%5E-%7Df(z)%20%5C%20dz%3D0$

$%5C%5C%5Cint_%7BC_0%7Df(z)%20%5C%20dz%3D%5Cint_%7BC_1%7Df(z)%20%5C%20dz%2B%5Cint_%7BC_2%7Df(z)%20%5C%20dz%2B%E2%80%A6%2B%5Cint_%7BC_n%7Df(z)%20%5C%20dz$

It tells us that the integral along the external boundary equals the sum of the integral along the internal boundaries.

If we want to prove this ,we just need to split the domain into two single-connective domains using line segments(or arcs)

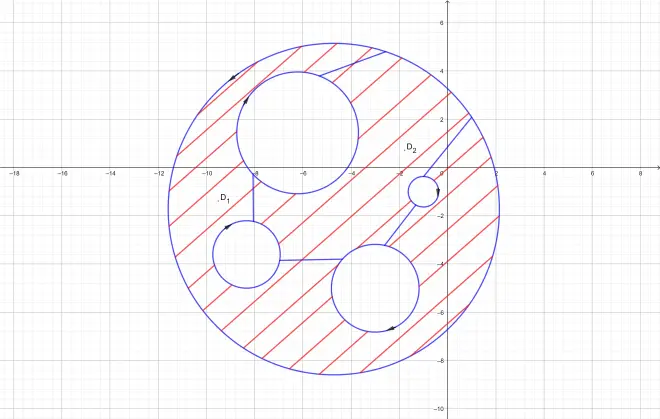
And use the former theorem concerning single-connective domain.Because that the integrals along the line segments(or arcs) can be offset,then we can find that the integral along zhe whole complex curve equals the integrals along the boundaries of the two single-connective domains.it's zero.

标签：

Calculus(88)——Cauchy-Goursat Theorem

Theorem on complex-connected domain

Calculus(88)——Cauchy-Goursat Theorem的评论 (共条)

你可能也喜欢这些文章

最新发布的文章

Calculus(88)——Cauchy-Goursat Theorem

Theorem on complex-connected domain

本文作者的其他文章

Calculus(88)——Cauchy-Goursat Theorem的评论 (共 条)

你可能也喜欢这些文章

最新发布的文章

Calculus(88)——Cauchy-Goursat Theorem的评论 (共条)