谜题规则介绍#16 涂黑类——数间(Heyawake)

这次来介绍一下另一个在日本很流行的题型——数间。

规则：涂黑一些格子，使得任何行列没有连续穿过两个区域边界的一段白格。黑格不能横竖相邻；所有白格横竖连通为一个整体。数字表示该区域中黑格数，数字可涂黑可留白。

例题：

规则里比较难理解的是“任何行列没有连续穿过两个区域边界的一段白格”这一段。简而言之，就是不能出现下图的这些情况，即“连续的一段白格之间不能有超过一条的粗线”：

数间的核心规则也是这一条最难以理解的规则。不过，下面大部分的技巧都是利用数字之间的结构来推的。因此，本文和仙人指路一文的写法会非常类似，会在文章中罗列出一些常用结构，然后进行分类处理。

1、任意区域的0。这种不需要图片吧。

2、区域内的极大值。

2.1、1*(2k+1)区域里的k。区域内第1，3，...，2k+1个格子涂黑。核心：相邻两个格子最多只有一个黑。

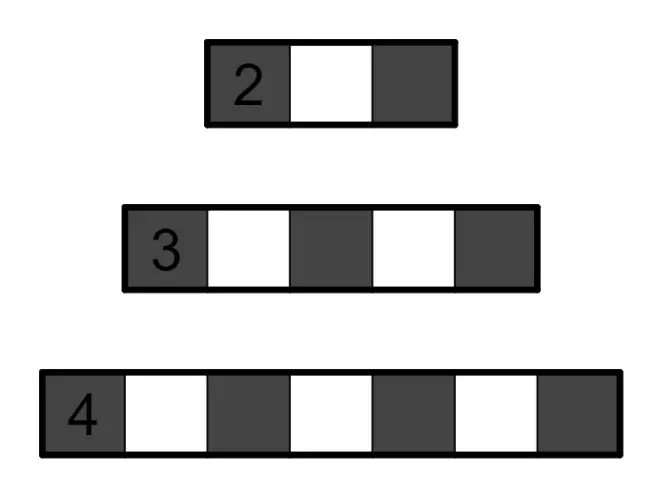
2.2、2*n区域里的n。一般来说这个时候会有两种填法，在某些特殊情况下除外，只有一种情况。不管是哪种情况，一定可以得到某些格子不能涂黑。

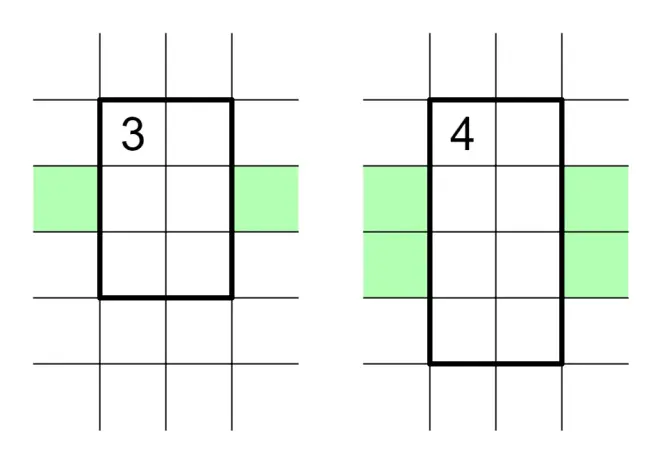
2.3、一些极大值或者极大值-1的情况。例如，3*3的5或者4，3*5的7等。

2.4、一些有限制的区域，如在边角位置，或者某些格子确定不能涂黑之后，可以得到更多的格子。这里由于不好表现，统一令下边是边界，且最左边的2位于左下角。另外，下图中区域和区域之间没有关联，仅仅是作为例子说明单个区域的情况。

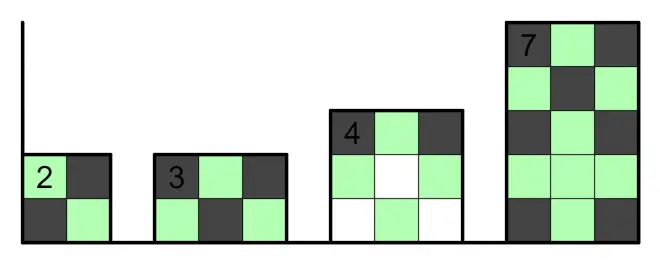
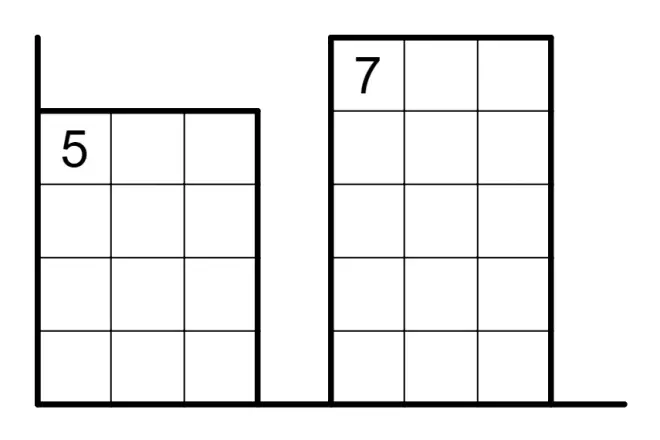
2.5、有些大区域可以采用分成小区域的方法来推出其的特殊性质。如上图中贴下边的3*5的7，可以分成上面的3*2和下面的3*3，上面最多3格黑，下面最多4格黑，两者都是极大值，组合一下便可以推出唯一情况。类似的情况还有角落上3*4的5。

3、白格连通性。

3.1、最简单的用法：涂黑某个格子会把白格分断，这一格一定是白。

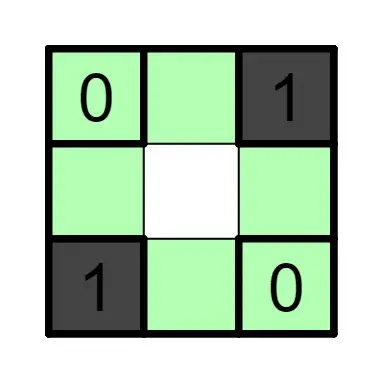
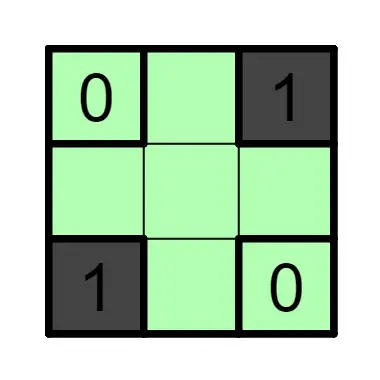
3.2、也很简单的用法：在某个区域的两种情况中，有一种情况会使白格分断成两部分，那么这个区域就只能是另一种情况。

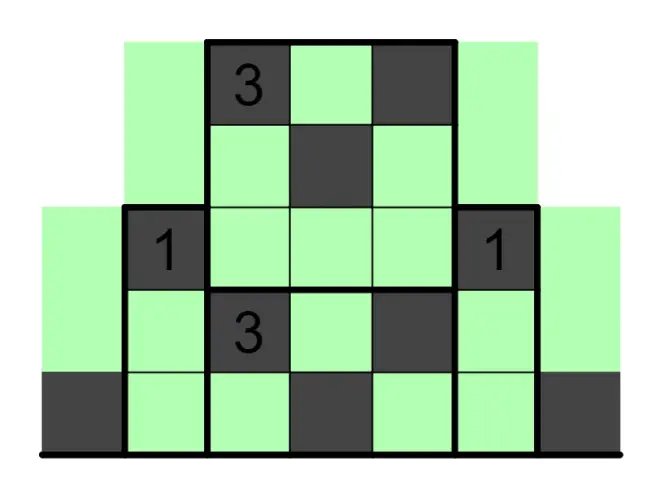
3.3、另一种比较复杂的用法是结合“白格不能连续穿过三个区域”来使用，解释起来比较复杂，见下图。

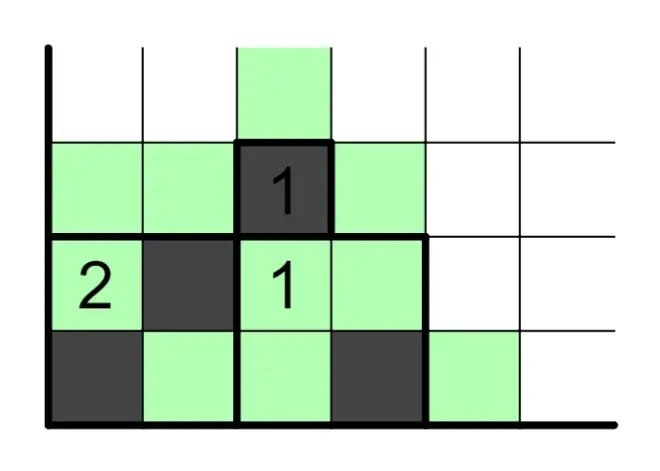
4、白格不能连续穿过三个区域

4.1、白格已经连续穿过了两个区域

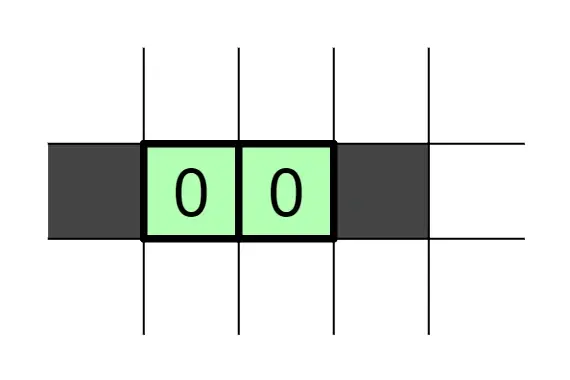
4.2、两段白格加起来穿过了三个区域

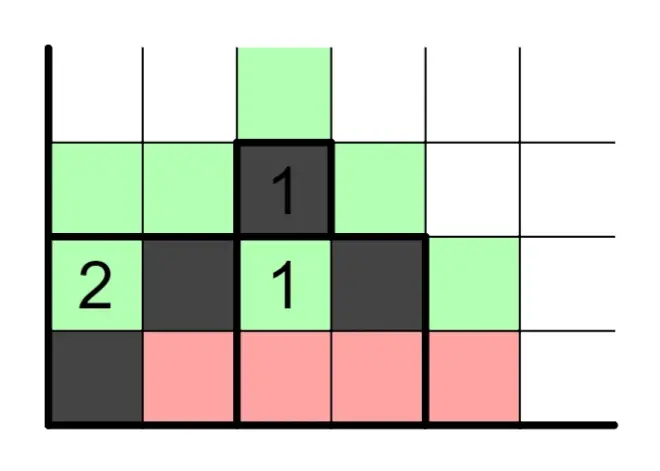
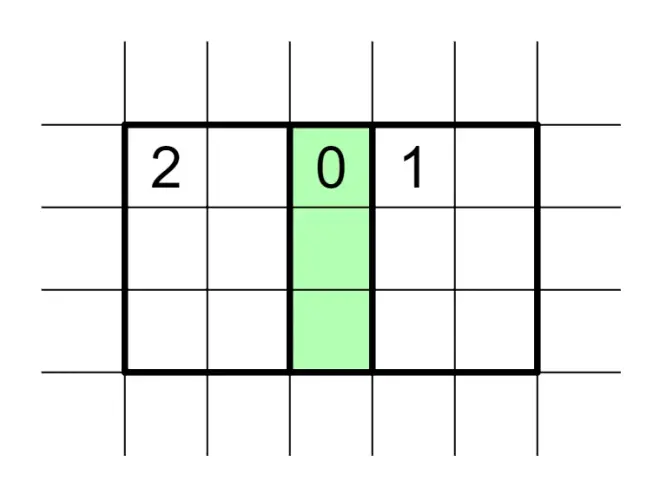
4.3、利用这条规则的一些极小值，如中间这一片0，它左边那列和右边那列的方格中至少要有一个涂黑（第二个图中除绿色外，同色格子必须有一个涂黑），那么至少要涂黑3个格子，而左右两个区域加起来最多涂黑3格，所以都只能落在颜色格子里，再判断一下就能确定涂色的位置。

基本技巧就讲这么多，其实有相当一部分技巧属于进阶技巧了。

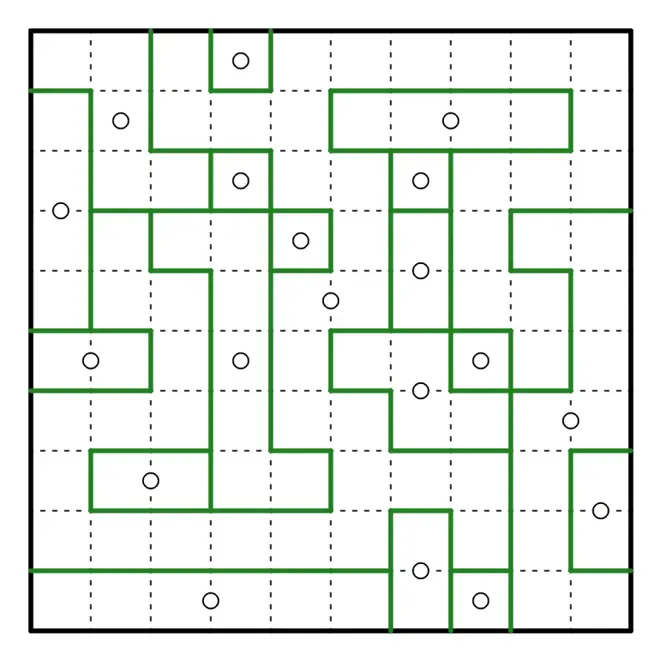
以下是两个练习题：

附上期答案：

这期写得比较久，因为工作了一直在咕咕，这一期的图也比较多。可能之后更新频率也不会太高，望大家见谅。那么我们下期见！