先给出结论：

对于任意一个n次方程Pn(x)=0

其中Pn(x)=a_0x^n+a_1x^(n-1)+......+a_(n-1)x+a_n

=Σ[n,k=0]a_kx^(n-k)

只要把x替换为y-n/na,就可消去n-1次项.

下面先看一次方程

ax+b=0   （a≠0)

我们看其函数形式y=ax+b的图像

不难看出，b是截距，当b=0时，方程永远经过(0,0),即方程的解恒为0,所以我们把函数图像平移至原点

ax+b-b=ax

故x恒为0，但我们不能直接加回去，因为这并不满足乘法分配律等性质，故需要变换

ax+b-b=a(x-b/a)+b

即令x=x-b/a,为了防止两个x混淆，故我一般用y代替右x.

因为此变换只与x有关，故算完x的值后可以直接代回关系式x=y-b/a,即可求出x的值.

再看二次方程

ax²+bx+c=0   (a≠0）

观察其对应函数图像

不难发现，当b=0时，图像的极值点在x=0上.

所以只要把极值点平移至x=0,即可消去二次项.

故需要先知道极值点的横坐标

这里给出两种方法，对称法与导数法，其中对称法门槛低，但导数法重要，后面都用导数法

①对称法

因为二次函数的图像具有轴对称性质，其极值点就在对称轴上，故只需求对称轴横坐标，而对称轴坐标可以直接用两根取平均值，即(x1+x2)/2,由韦达定理可得等于-b/2a,故这就是极值点横坐标.

②导数法

因为极值点导数为0，所以对其函数求导并令值为0，其x值为横坐标.

(ax²+bx+c)'=0

          2ax+b=0

                  x=-b/2a

求完横坐标后，令x=y-b/2a,即可消去二次项

三次方程同理，但是要求二阶导得其拐点。现在开始证明n次方程的情况并解释为什么要求二阶导.

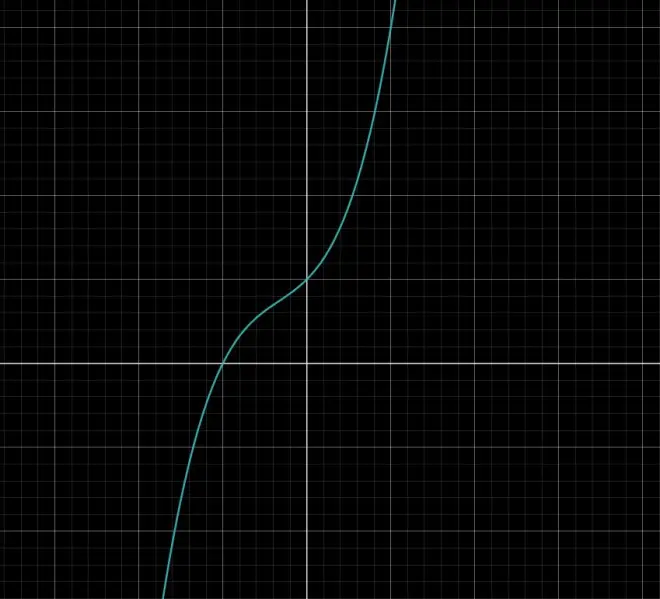
根据高斯代数基本定理推论，一个n次方程有且仅有n个根，因为这些根与x轴交点都为0，根据罗尔中值定理（或拉格朗日中值定理），每两个根间都有一个斜率为0的点，故对于三次及以上的方程，求一次导后会出现多个值，此时需要求多次导，直到值唯一，即变为一次方程.因为每求一次导方程就降一次，故设要求x次导方程才变为一次方程.则n-x=1,解得x=n-1,所以要求n-1阶导.

又因为求完n-1阶导后只剩n与n-1次项，

即n!ax+b(n-1)!=0

                n!ax=-b(n-1)!

                   ax=-b/n

                     x=-b/na

故-b/na就是需要平移的距离，即要令x=y-b/na. 

证毕

此证明可能有些不严谨，请见谅.