深入理解和运用主成分分析（PCA）

主成分分析（PCA）可以对相关变量进行归类，从而降低数据维度，提高对数据的理解。

身边的人基本上都会主成分分析，我对它的感觉是，PCA虽然被广泛使用，但是真正理解它的人却很少。大部分人使用数据代码，咔咔一顿分析，却很少理解产出的结果。

本期的目的就是说清楚PCA的概念和使用方法。

01 主成分分析简介

主成分分析顾名思义就是寻找主成分的过程。主成分是什么呢？

主成分可以认为是特征的规范性线性组合。在一个数据集中，第一个主成分就是能够最大程度解释数据中方差的特征线性组合。第二个主成分是在与第一主成分垂直这个限制条件下，最大程度解释数据中的方差。其后的每一个主成分都遵循同样的规则。

因此，可以看出，PCA中的线性组合是一个关键假设。如果你有一堆变量之间基本上不相关的数据集，用PCA分析就会得到毫无意义的分析结果。另一个关键的假设是，你使用的数据应该服从正态分布，这样协方差矩阵即可充分描述数据集。PCA对非正态分布的数据具有相当强的鲁棒性，甚至适用于二值变量。

如何理解特征的线性组合呢？假设有一个数据集，有两个变量，数据集的分布图如下：

每一个菱形代表一个观测，数据已经被标准化为均值为0、方差为1，因此数据正好组成一个椭圆形。

我们画一个水平短线，使得数据在X轴上具有最大方差，这个主成分就是两个变量的线性组合，表示为：

PC1 = a11X1+a12X2

这个主成分建立了一个基准方向，在这个方向上，数据差异最大。

同样用同样的方式得出第二主成分，只是它与第一主成分不相关，方向与第一主成分是垂直的。如下所示：

02 PCA分析流程

（1）变量标准化

对变量进行数据标准化是PCA的第一步。这主要是解决初始变量之间存在很大的差异的问题。

默认情况下，函数scale()对矩阵或数据框的指定列进行均值为0、标准差为1的标准化：

（2）降维

降维是PCA的核心。如何理解降维呢？比如，你有30个变量，使用PCA可将30个相关（很可能冗余）的环境变量转化为5个无关的成分变量，并且尽可能地保留原始数据集的信息。

这个时候有几个核心概念：

①特征向量

特征向量是方差最大（信息最多）的轴的方向，称之为主成分。

②特征值

特征值为某个主成分的方差，其相对比例可理解为方差解释度或贡献值。特征值从第一主成分会逐渐减少。

③载荷

载荷是特征向量乘以特征值的平方根。载荷是每个主成分上各个原始变量的权重系数。

03 R语言中用于PCA的包

目前来讲，主要有5个包用于PCA的计算：

（1）stats默认加载包，提供procomp()与princomp()函数。

（2）psych包，提供principal()函数。

（3）FactoMineR包，提供PCA()函数。

（4）ade4包duli.pca()函数。

（5）vegan包的rda()函数。

不同的包计算出的PCA结果会有一点差别。

04 如何用R语言完成主成分分析

这里我推荐大家学习《R语言实战》和《数量生态学（第二版）》的例子来加深大家对PCA的理解。

4.1 Psych包做PCA

（1）首先我用psych包来演示PCA分析。数据用的R语言中自带的iris数据集，

该数据包含3个鸢尾花物种的50个样本，且每个样本中测量了4个特征，即萼片和花瓣的长度和宽度。

我们需要对数据进行标准化，使数据的均值为0，标准差为1。完成标准化后，使用psych包提供的cor.plot()函数，创建一个输入特征的相关性统计图。

可以看出萼片的长度与花瓣的长宽存在正相关关系，萼片的宽度与花瓣的长宽存在负相关关系，因此，这个数据集非常适合提取主成分。

（2）接下来，进行PCA分析

可以调用函数生成的pca对象检查各个成分，但我们的主要目的是确定要保留的成分的数量。为此，使用碎石图即可。碎石图可以帮助你评估能解释大部分数据方差的主成分，它用X轴表示主成分的数量，用Y轴表示相应的特征值。

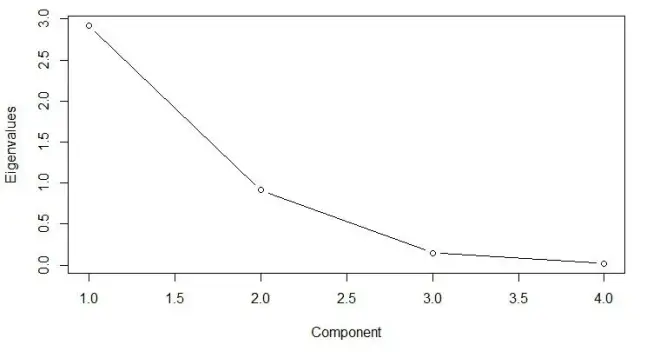
需要在碎石图中找出使得变化率降低的那个点。从这个图可以看出，3个左右的主成分是可以的。

（3）正交旋转与解释

旋转背后的意义是使变量在某个主成分上的载荷最大化，这样可以减少（或消灭）主成分之间的相关性，有助于对主成分的解释。进行正交旋转的方法称为“方差最大法”。

这里我们设定使用3个主成分，并需要进行正交旋转。

如何看输出结果呢？

输出中有两个部分比较重要，第一部分就是3个主成分中每个主成分的变量载荷，分别标注为RC1至RC3。对于第一个主成分，变量Petal.width具有非常高的正载荷,对于第二个主成分，变量Sepal.Length具有非常高的正载荷。

第二个重要部分，就是以平方和SS loading开始的表格，SS loading中的值是每个主成分的特征值。如果对特征值进行标准化，就可以得到Proportion Explained行。这一行表示的是每个主成分解释的方差的比例。可以看到，对于旋转后的3个主成分能够解释的所有方差，第一个主成分可以解释其中的44%，一般来讲，你选择的主成分应该至少解释大约80%的全部方差（经验数据）。查看Cumulative Var行可以知道，这3个旋转后的主成分可以解释99%的全部方差（我们的数据实际上可能并不会这么好）。所以我们可以充满信心地认为，已经找到了合适数量的主成分。

我们用ggplot2来可视化PCA的结果：

可以看出三个物种在PCA上具有显著性的区别。

4.2 FactoMineR包做PCA

个人觉得FactoMineR包做PCA更为强大。FactoMineR包来做PCA，并使用factoextra来提取并可视化结果。数据同样用的是iris的数据。

（1）PCA运算和结果

具体的结果我们可以通过summary()得到。

第一个PC解释了72.96%的方差，第二个PC解释了22.85%的方差。前两个主成分累积解释了96%的方差。

可以使用factoextra包的各个函数来提取变量的分析结果。

（2）碎石图选取主成分

为了更直观地展示每个主成分解释的方差，我们可以使用函数fviz_screeplot()绘制所谓的碎石图(screeplot)。

根据前面我们讲的经验原则，希望提取的主成分累积解释超过80%的方差（我看到也有人说是70%）。另外，我们希望提取的特征值大于1。

可以用get_eigenvalue()函数帮我们提取特征值。

可视化特征值：

由此可见，我们只需要提取前两个主成分就行了。

（3）可视化PCA

在做可视化之前，要讨论一下PCA可视化的类型：

首先，当前两个主成分解释数据中大部分方差时，你可以通过将观测值投影到前两个主成分的范围上来可视化数据。在PCA中，此图称为分数图（得分图）。你还可以将变量向量投影到主成分的范围上，这称为载荷图。

PCA得分图是一个散点图，是用于可视化不同样本之间相对位置的图。而载荷图是几个向量构成的图，显示了变量和主成分之间的关系。如下所示，我们可以观察到PetalWidth和PetalLength在x轴的投影较大，而在y轴上投影较小，说明它们对第一个主成分轴的贡献高，而PetalWidth和PetalLength的夹角较小，说明它们密切相关。

双标图：得分图+载荷图。一个双标图展示了以下信息：

点是行（案例/样本），向量是列（变量）。两个点之间的距离近似于它们的相似性。向量长度近似于变量的标准差。两个向量之间的余弦近似于变量之间的相关性。

①PCA得分图：观测值坐标图对应了factoextra包中的fviz_pca_ind()函数

首先，我们画得分图。这里我们使用物种信息来着色和分组。

②PCA载荷图：

这里展示了变量对主成分的贡献值。

同样地，我们可以使用cos2这个指标，cos2反映了各个主成分中各个变量的代表性。一个变量的所有主成分cos2值加起来等于1。对于主成分而言，某个变量的cos2越接近1，则说明变量对该主成分的代表性越高；cos2越接近0，则说明变量对该主成分的代表性越差。

较高的 cos2 表示变量在主成分上有良好的代表性。在这种情况下，变量的位置靠近相关圆的圆周。反之，低 cos2 表示变量未由 PC 完美表示。在这种情况下，变量靠近圆心。

③双标图：

双标图可能是最常用的，fviz_pca_biplot（）函数完成双标图：

这里展示优化后的双标图：

4.3 Vegan包做PCA

这里展示的是《数量生态学》中的案例，但为了方便比较，用的数据还是iris的数据集。

同样可以看到，前两个主成分解释了96%的方差。

用碎石图判断选择多少个排序轴

绘制样方和变量的双序图

双序图中第一种设定参数scaling = 1（最优化展示对象之间的距离），第二个设定scaling = 2（最优化展示变量之间的协方差）。

5 总结

PCA不是统计分析，而是一种探索性分析的方法。做这一期内容我也学习到了PCA的复杂性，有很多地方没有阐述明白的，希望大家见谅，我推荐大家学习《数量生态学》第二版的内容。

点点关注，加入我们吧~