标量场量子化

我们利用正则量子化的方法量子化上一节中的标量场，并且有以下的对易关系：

其中\pi是真正共轭变量。

对于上一节中的K-G方程的解，和他们的共轭形式。我们可以将场展开为：

注意这里的求和，还没有改为积分。然后根据等时对易关系，我们可以得到产生湮灭算符的对易关系：

在Heisenberg绘景中，量子态在Hilbert空间中。我们可以利用Fock表象来表示态，并且利用Dirac左右失标记它。则根据湮灭算符的性质会有真空态的定义：

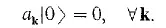
等式左边就表示湮灭算符作用在真空态上美欧任何的结果。而产生算符作用在真空态上会产生一个粒子：

类似的对于更多不同的模式可以作用不同模式的产生算符到真空态上。如果是同一模式的多粒子态，就要注意态的归一化系数。

产生湮灭算符作用在数态的结果可以表示为：

这是在实际的计算中会经常使用。

Fock表象的态在计算中是很实用的，可以简化计算的过程。