插值与拟合
插值与拟合
引言:我们经常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,例如数据拟合、参数估计、插值等数据处理算法。此类问题在MATLAB中有很多现成的函数可以调用,熟悉MATLAB,这些方法都能游刃有余的用好。

插值法
1. 插值的基本原理
在实际中,常常要处理由实验或测量所得到的一些离散数据。插值与拟合方法就是要通过这些数据去确定某一类已知函数的参数或寻求某个近似函数,使所得到的近似函数与已知数据有较高的拟合精度。 如果要求这个近似函数(曲线或曲面)经过所已知的所有数据点,则称此类问题为插值问题。 (不需要函数表达式)
2.插值方法
选用不同类型的插值函数,逼近的效果就不同,一般有:
(1)分段线性插值(二维插值)
(2)Hermite插值
(3)样条插值(二维插值)
(4)拉格朗日插值算法(一维插值)
(5)牛顿插值
如果使用拉格朗日插值或者牛顿插值等一段插值算法,使用均匀节点构造高次多项式差值时,在插值区间的边缘的误差可能造成龙格现象。它是由Runge在研究多项式差值的误差时发现的,这一发现很重要,因为它表明,并不是插值多项式的阶数越高,效果就会越好。

(1)分段线性插值

方法:分段线性将每两个相邻的节点用直线连起来,如此形成的一条折线就是分段线性插值函数。计算点的插值时,只用到左右的两个节点,计算量与节点个数n无关。
假设两个节点为(x1,y1)和(x2,y2),则该区间上的一次线性方程为:

证明过程:


知识点:
a.分段线性插值运算量较小,插值误差较小,插值函数具有连续性,但是由于在已知点的斜率是不变的,所以导致插值结果不光滑,存在角点。
b.分段线性插值存在较好的收敛性,n越大,即分段越多,插值的误差也就越小,函数收敛越接近原函数
插值的MATLAB实现

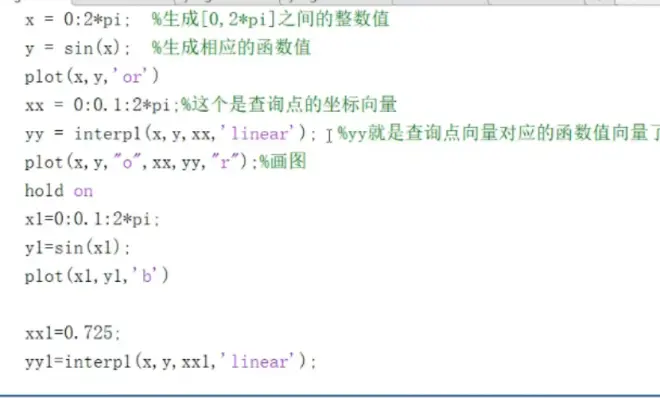
图像结果如下:

(2)分段三次Hermite插值



Hermite 插值就是要求插值函数不仅经过所给节点,而且要保证在该点的导数也相等。
以3个点为例,想要使用分段3次Hermite 插值求出这三个点的插值函数:
分析一下,每一段三次hermite插值多项式
都有4个未知系数需要求解,三个点就是两段,那么就有2*4=8个未知数。8个未知数,就需要联立8元一次方程组,需要8个方程:
一阶导数值相等
上面有5个方程,还差3个方程,这三个方程从定义中可知,需要知道每个点x 0 、 x 1 、 x 2
即的导数值必须已知,但是实际工程中是不太可能知道每个点的导数值的。因为,你连原函数都不知道,怎么能知道导数值呢?
总结一下:Hermite插值在实际使用的时候没有多大意义,同时知道点和导数,还假装不知道原函数的情况,不多(PS:都知道导数了有什么计算的必要?)
插值的MATLAB实现


分段三次Hermite插值的所有代码

(2)三次样条插值



样条函数是一个重要的逼近工具,在插值、数值微分、曲线拟合方面有着广泛的应用。
在引出样条插值的详细内容之前,我们来看看之前的插值方式的优缺点。
插值方式优点缺点多项式Lagrange插值整体性强,光滑性好不一定收敛分段多项式Lagrange插值局部性好,收敛性保证光滑性差(相邻区间点处不可导,尖点)分段多项式Hermite插值局部性好,满足一定光滑性,收敛性得到保证需要倒数信息
为了集合上述方法的优点避免缺点,我们就提出了样条插值法。样条插值是一个收敛性好,光滑性好,不需要过多导数信息,只要函数值信息的插值方法。
用一句话来讲:
三次样条插值就是将原始长序列分割成若干段构造多个三次函数(每段一个),使得分段的衔接处具有二阶导数连续的性质(也就是光滑衔接)。
插值的MATLAB实现

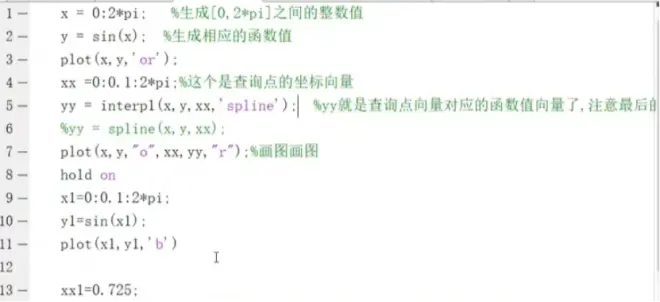
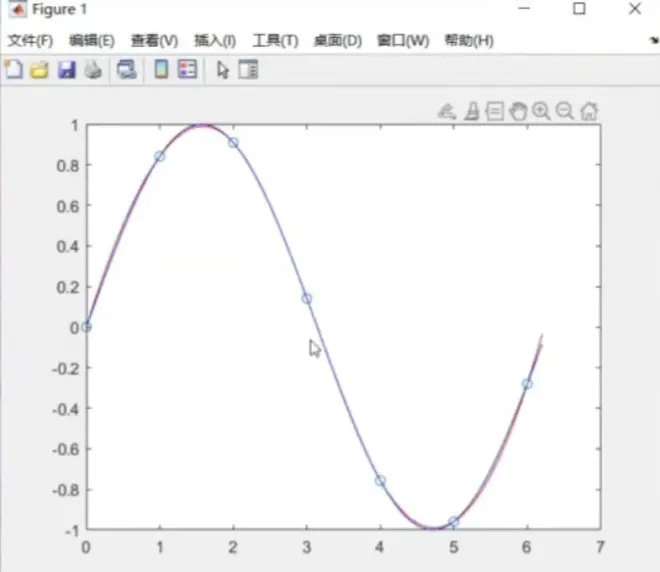
各个插值优缺点:

1.2. 拟合的基本原理
如果不要求近似函数通过所有数据点,而是要求它能较好地反映数据变化规律的近似函数的方法称为数据拟合。(必须有函数表达式) 近似函数不一定(曲线或曲面)通过所有的数据点。

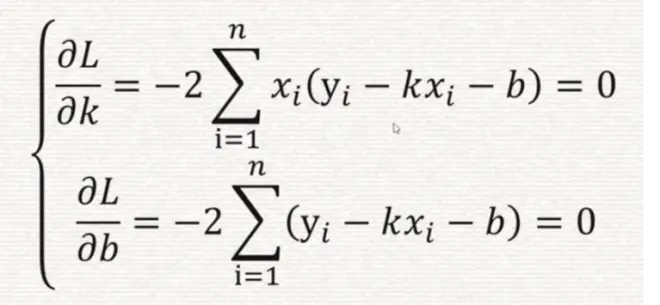


拟合的MATLAB实现



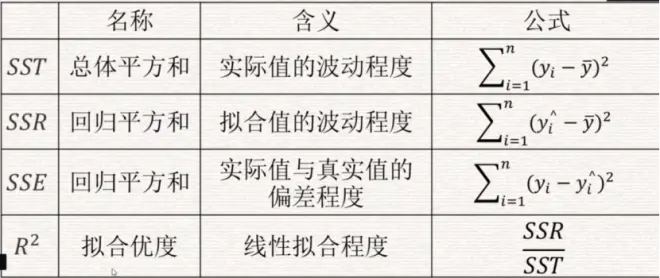
拟合评价操作方法:
1. 公式计算
2. cftool
3. 图像->基本拟合
3.1、联系
都是根据实际中一组已知数据来构造一个能够反映数据变化规律的近似函数的方法。
3.2、区别
插值问题不一定得到近似函数的表达形式,仅通过插值方法找到未知点对应的值。数据拟合要求得到一个具体的近似函数的表达式。
3.3、选择
当数据量不够,数据量<30,需要补充,且认定已有数据可信时,通常利用函数插值方法。
实际问题当中碰到的函数 f (x) 是各种各样的,有的表达式很复杂,有的甚至给不出数学的式子,只提供了一些离散数据,警如,某些点上的函数值和导数值。
参考视频来源于bilibli:https://www.bilibili.com/video/BV13T4y1r7R1/?spm_id_from=333.337.search-card.all.click
借鉴文章链接来源于csdn:https://blog.csdn.net/u011754972/article/details/123550131

