中考数学【二次函数】核心方法梳理(偏压轴)|期末救急

大家好呀
提到二次函数相信很多人都很怕
因为不管在中考的小题还是大题
他经常作为压轴题出现
实际上他的考法我们总结一下
无外乎就这么几种
所以说我们逐一突破其实也就那样吧
那么趁着期末来临之际
我们复习一下
它最重要的一些方法与考点
那么第一对于一个二次函数而言
它的解析是有哪一些解法呀
这是最基础的
除开一般式
还有顶点式是最最常见的
因为很多时候
我们都会与它的根打交道
另外如果题目给了你顶点
那么可能我们会用顶点式去解决
此时二次函数的顶点坐标就是HK

但我们光知道定义远远不够
还得知道a b c代表的含义
比方说a
我们当然知道
a大于0的时候开口向上
a小于0的时候开口向下还不够
比方说a的值有什么含义
a的绝对值越大呀
它虽然依然开口方向不变
但是开口会越来越窄
比方说a大于0的时候随着a增大
它的增长速率就会越来越大
所以变窄了嘛
那b控制着什么呢
控制着对称轴的位置
x等于负的r a分之b
所以题目如果给了你一些图像问题
他要你判断什么a和b的关系
你一定要看看对称轴是大于0小于0啊
或者说等于一个特殊的值
等等c控制是什么
与y轴的一个焦点
所以你令x等于0得到的函数值就是c
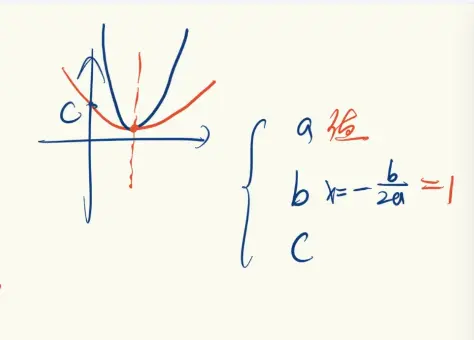
我们知道了这个
其实还得知道一点额外的意义啊
有的时候他中考压轴题小题的压轴啊
喜欢这样考
比方说
对于一个开口向上的二次函数
他说在某一个点处的函数值
比另外一个点处的函数值要大
意味着什么呢
我们该如何翻译这个条件呢
比方说这个点设为X1 Y1这个点设为X2 Y2
题目说Y1是大于Y2的
那我们可以得到横坐标的什么关系啊
那么我们可以发现
二次函数是一个轴对称图形
所以想让它的纵坐标越大呀
我们只需要保证距离对称轴的距离越远就行了
所以说想满足纵坐标的值比他大
我们只需要满足什么
他的横坐标到对称轴的距离
大于另外一个点
横坐标到对称轴的距离吧
那么它到对称轴的距离是多少呢
我们把对称轴设为x等于a
就是等于两个横坐标叉折的绝对值
只要大于x 2减a的绝对值就行了吧

好这是我们说的性质定义
不妨就小试牛刀
举一个中考题为一个例子
2021年浙江中考
题目看着很长但是做起来很简单
我们画一个图就可以搞定了
题目说给了一个抛物线
它与x轴的焦点分别是10和30
哎
那有可能开口向上有可能开口向下
我们不妨先画一个开口向上的
因为向下是一个道理
那比方说就是这样的一个抛物线喽
他说
P1和P2是抛物线上不同于a b的两个点
随便点两
个点
比方说P1在这P2在这g P1 a b的面积为S1
PR AB的面积为S2
我们可以发现这两个三角形是什么
是同底但是不等高对吧
底都是AB
高的话就是这两个的纵坐标的绝对值
其实挺好理解吧
然后说下列4个结论
我们主要看三结论和四结论
那么三结论来看看他说的啥啊
他说当x 1-2的绝对值大于x
2-2的绝对值大于1的时候
有X1大于X2
那么第一个问题他为什么要写个减2
你一定要弄清楚
弄清楚了其实就搞定了
那第一这里是1这里是32是啥呀
2是他对称轴的横坐标
所以说这句话它表达的是什么含义
它代表的是
P1点的横坐标到对称轴的距离
对吗你知道了这一点的话
这一题不就清晰很多吗
它代表的是P1的横坐标到对称轴距离
那这个呢
它代表的是P2这个点到对称轴的距离
所以题目表达的含义是
P1到对称轴的距离
大于P2到对称轴的距离
并且还要大于1
那他为啥要给大于1这个条件呢
如果这个距离就等于1
P1什么时候到对称轴的距离等于1啊
也就是说他在a这个点的位置的时候
好我们就明白了
所以说
P1和P2到对称轴的距离都是大于1的
那么P1和P2都不会再y
应该说x轴的下方吧
这是他想表达的含义
那么他说则S1大于S2
那么由我们刚才说的这一个点
我们就可以知道
呃是不是应该有Y1一定大于Y2呀
那有Y1大于Y2
S1和S2的关系还不好搞定吗
我们来看S1等于多少
S1也就是这个三角形的面积
等于1/2倍的底边a b的长度
然后再乘以高它的高是多少呢
是Y1 由于这个距离是大于1的
所以Y1一定是大于0的
P1和P2都一定在x轴的上方嘛
那么S2呢
它是不是等于a b的绝对值乘以Y2呀
那所以Y1 S1当然大于S2了
因为Y1大于Y2嘛
所以3是对的
那么4当然错了
1和2他们两个其实都不确定
所以这道题只有3是对的
如果开口向下呢
完全相同的道理
距离对称轴越远
那么我们得到这个y的绝对值呀
它就越大
那么对应的这个三角形的面积
当然也是越大了

好
这是我们说的它一个简单的一个性质
接下来我们再来看关于a b c的题
它有时候会做一些压轴题
出现选择压轴题
这种题基本就送分题了
那么第一给出来这种性质
我们的第一想法是什么呢
是负值比方说他问你a加b加c等于0
那我问你你负x等于多少的时候
你可以把右边变为a加b加c
太简单了
x等于1的时候
那么x等于1的时候右边是
是不是又变为了a加b加c
那我们只用看看x等于1的时候函数
值怎么样啊
它恰好等于0
所以它确实等于0对吧
因为x等于的时候y等于0嘛
那第一个是成立的
这个你就会遇见问题
你说好呀那我也复职呗
那我问你x等于多少的时候
它会变成这个样子呀
那你就抓耳挠腮想半天对吧
那么对于这种系数不规则的
有一个非常通用的方法
就是比较笨的方法
你把所有的东西都转化为a
基本上一定能够做出来
那怎么转呢
我们比方说来看b
b和a的关系通过什么来确定
通过对称轴的位置
对称轴是什么
是负的2A分之b
在这一题中对称轴等于多少
等于-1
所以马上可以得到b是等于2A的
那么c与a的关系怎么确定呢
那么最开始这里不是还有一个式子吗
把这里往上面一带
那么b是等于2A
所以3A加c等于0
所以c是等于负3A
那么他给的这个式子是不是就变为了
a减去4A加上负3A
它要大于0
那么这一个对不对啊
显然我们马上就可以知道
哎有问题对吧
这个地方得到是负6A吧
因为a是大于0的开口向上嘛
所以负6A是小于0的
40粗的
那么这道题其实剩余的也比较简单了
因为2一眼就能看出来是个错的
b是等于2A的
所以只能是1和3是对的
四个选项中每个选项都只有2个啊
所以是1和3

到此为止我们都讲的比较
简单他出现了都是简单的压轴题
那有的时候他会出的难一点点
比方说与根的关系
首先
我们得知道二次函数什么时候有根
什么时候没有根
这点非常好判断
我们只需要另外等于0
得到一个一元二次方程
这个一元二次方程的DORT小于0的时候
它与x时候就没有焦点
那么DORT等于0的时候正好相切
有一个焦点
DORT大于0的时候是有两个焦点对吧
好那现在我问你个问题
如果一个题目他说
对于一个二次函数啊
它永远大于等于0意味着什么呢
一个二次函数永远大于等于0
意味着二次函数它永远在x轴的上方
或者说与x轴相切
所以意味着DIRT永远要小于等于0
因为最多只有一个焦点
或者说没有焦点
没有焦点的时候dirt就小于0对吧
我们就此就可以得到
跟有没有这种简单的联系啊

等一下我们还会讲韦达定理
也就是根与细数的关系
现在我们再来看一道哎比较出名的
广东的一道
大题的压轴题
这道题很多人第一问没有做出来
第一问做出来第二问其实就没有
太难了他给了一个这个东西
又给了个连不等式
然后要你求他的解析式
那么他说过-10这个倒挺简单
-10你把1带入
是不是得到a b c的一个关系
那么这一个横成立的一个式子
我们怎么去处理它呢
有一个最笨的方法就是它横成立
得到一个关系DIRT
的关系对吧
这个横成立
又可以得到一个DIRT的关系
可以强行解出来
但是那样做太累了
我们可以化解一下
中间是我们不知道的一个位置函数
但是两边是知道的呀
这
我们对这两边都可以进行一下化减的
右边明显可以使用因式分解吧
我们提个2出来
它就是x方减去4X加上3
所以我们可以将它因式分解为是x
减1乘以
x减3吧这两边是不是一样的式子
那右边左边这里不是相同的道理吗
它也可以变一下
我们提个4出来
那么得到就是4倍的x减3
我这样一提
其实有一个线索非常的明显
这里有什么x减3
右边也有x减3
那我试问你在x等于3的时候
这两个式子是不是都等于0啊
那x等于3的时候中间的式子为多少呢
只能也为0啊
因为一个数大于等于0
小于等于0它肯定就等于0了吧
所以我们只要把握这一点
这题就可以做的轻松很多
在x等于3的时候
这个二次函数它也为0
那么这个二次函数
它是不是一定过30这个点
而这个二次函数又过-10这个点
那我试问你
这个二次函数你说怎么设最方便啊
那当然是用两根式了
那么是不是设为是x减去3乘以x
加上1啊
那么设了一个两根式
再如何通过它再得到一个方程
把a给解出来呢
那么与左边连力会简单点
与右边连力可以
做但有点麻烦
这边是现成的呢
左边是个依次函数
我们用代数的思想是最明显的
就是不用什么相切的思路
题目说的是这个式子是横成立的
那么既然是横成立
我们将它全部都移到右边去
变为一个二次函数横成立的问题
这样研究起来更加的方便
那么减去2A
再加上4我把它提一下
然后再减去3A加上12
它大于等于0
横成立
那么一个二次函数想大于等于0
很成立只需要满足两个条件
第一a是大于0开口向上
那么a等于0行不行
不行等于0不是二次函数
第二does TA得小于等于0
我们基于这两点
其实答案已经做出来了
有人说does TA小于等于0
不是一个不等式吗
你可以试一下
因为如果你画个图的话
你会发现肯定是相切的情况
我们先试一下
然后我再画一个图辅助理解
b方减去4 a C a c
得到是不是就是这一串
那么得到的就是4 a方加上16倍的a
加上16 然后减去48倍的a加上
呃负负得正加上12倍的a的平方
那我们将它整理一下
是不是16 a方减去32 a加上16啊
好家伙
提个16出来变为16倍的a减1的平方
它是小于等于0的一个完全平方数
小于等于0是不是
完全平方数只能等于0
所以a等于1
那么a等于1出来了
1带回去是不是就做完了
好那有人说呃
如果我不想
用代数思想呢
你画个图这道题也可以出来
比方说左边是什么
是一条直线
它是过30斜率为4的一条直线
那么再来看右边
因为为什么要画这两个
这两个能画出来呀
中间画不出来嘛
那右边的这一个二次函数是什么
是过13这两个点的
这里是30嘛
这里是10
所以它是这样的一个二次函数
那么
由于这个二次函数永远大于等于他
这个是肯定成立的
不然题目就错了对吧
实际上我们画出来马上就能知道
这个二次函数与这个直线
其实是相切的
那么中间的二次函数
与这个直线当然也只能是相切的啦
它为了在二次函数的下方
而又在这个直线的上方
它只能是这样画的一个图像
另外交的一个点就是-10
那我们知道了
既然中间的这个函数它是这样的图像
当然就知道了它与这个直线相切
那么什么时候是相切啊
就是说
我们令直线与二次函数连力的时候
得到得到的Derta只能等于0
Derta等于0直线与二次函数就相切吧
好那么相切其实还有个快速求
切线直线斜绿的方法
这个我就不说了呃
免得二字结论太多了大家听得难受

那么根我们还可以更深一步
就是根与细数的关系
我们利用y等于0
可以得到一个关于x的一元二次方程
有的时候题目他要你求一些值
是关于两个根对称的
一些代数式求和啊
什么求集什么的
此时你用根与系数的关系
就可以做出来了

那么这类题我们同样举一个呃
去年中考的一道真题来举个例子
压轴题
这是2018年大庆市的中考压轴题
看着很复杂我们直接做他的最后一问
关键信息我都给出来了
那么他说的这个东西看的也很头秃
我现在就把它改变为一个
大家都能够听懂的
一个马上就能够知道他在说什么
他给了一个二次函数
二次函数的解析式就是他
所以过的两个点呢是40和00
那么另外一方面呢
过一个定点F20呢
我们随便做一个直线
它与这个二次函数
是不是交于了两个点呢
把这两个点设为m点和n点
我们将m的坐标设为X1和Y1
将n点的坐标设为X2和Y2
那么题目问的这个东西
其实马上就可以变为是要我们求
Y1加上1/2加上Y2加1/2是等于一个定值
如果你不信的话你可以算一下
这道题倒还有点难的
那我们要求他是定值
Y1和Y2是什么
是这个直线与抛物线焦点的重坐标
对吧
那往往涉及到这种焦点的代数值啊
基本上都是可以考虑
根与系数的关系就是伟大定理了
怎么办呢
在做之前我们先可以通分一下
明确目标嘛
通分以后
分子分母就是Y1乘加Y2加2乘以Y2加2
然后分子呢就变为是Y1加Y2
然后再加上数字4
来看看分母啊
分母得到的就是Y1乘以Y2加上
两倍的Y1加Y2加上4
而分子呢
Y1加Y2加上
4发现了没有
这些都是维达定理中间的项吧
所以我们只需要令直线与抛物线连力
最后
把这些东西都用伟大定理表示出来
答案一定可以做出来
那怎么与伟大定理连力呢
我们来试一下呗
这个直线方程可以设出来
设y等于k倍的过20嘛
那么就可以设为是k倍的x减2
那么这个抛
物线的方程当然也可以写在这里了
我可以把它改写一下看的好看一点
是4Y等于x方减去4X
那么我们将它与直线连力
就可以得到关于x
或者说关于y的运用
x方程那要得到哪一个呢
我们要求的是Y1和Y2的关系
所以你一定是消掉x得到y
虽然削掉x要麻烦一点点
但是必须得削它才能得到我们的目标
那么第二个式子除以k
然后再加上2
是不是就可以得到x与y的关系了
我们将它带入第一个式子
就可以得到关于y的一元二次方程
你不要慌啊
这个关于y的一元二次方程
其实挺简单的
那么得到k分之y加上2的平方
然后再减去4倍的x
也就是k分之y加上2
哎将两边打开以后先把右边打开吧
右边打开就是得到k方
y方加上4Y除以k加上4减去k分之4
y减去8
两边是不是可以同时乘以k方啊
乘以k方以后右边得到的就
是y方那么还乘以k方这两项没了
这个乘以k方以后是减去4倍的k方
y我直接把它移到右边去了
那这两个再减去k方以后
呃这两个相减是-4
乘以k方是-4倍的k方
是不是马上就可以得到
Y1加Y2和Y1乘以Y2了
Y1加Y2是等于负的a分之b
也就是等于4倍的k方
那么Y1乘以Y2呢
是等于a分之c也就是负4K方
将它往上面带得到真的是一个定制
那么分子得到是什么
是4K方加4吗
Y1加Y24K方
那么Y1乘以Y2呢
是等于负的4K方
Y1加Y2是等于4K方
乘以2得到是8倍的k方再加4
这一个相加得到等于多少
是不是4K方加4和分子相等
所以说它就等于一定值
是不是证明完毕了
所以说关于维达定理的运用
我们也需要熟悉

那么我们上面都是讲的关于二次函数
一些本身的代数关系
有的时候它会与别的相结合
而最常见的就是与什么将军一马
胡不归 20元相结合
得到的最值
相关问题
或者说
要你问什么时候形成平行四边形
正方形矩形等等的特殊图形问题
两种都考的算多的底下考的最多
我们先来看最直
那么最直问题你只需要把握一个点
就是对称的思想
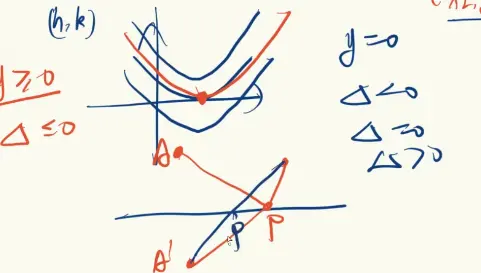
我们简单回顾一下将军一马模型
他就是说给了两个定点嘛
然后这个定点先引一个线段到这
个蓝色的线段上
然后再弹回去
问这个之和什么时候最短
这两个线段之和
那怎么去做
我们是过这个点
做底下这个点运动轨迹
的这个线段的一个对称点
我们把过a啊
做这个蓝色线段对称点为a撇
那么这个a p和a撇p的长度是相等的
所以它加它就变为了是这个加这个
那么这两个折绣呢
相加什么时候最短呀
当然就是两点之间距离最短了
所以说点p在这的时候最短对吧
那往往作为压轴题的时候
他可能会有多个点
但是我们的思想与方法没有变化
比方说我们来看这一道题啊
同样是刚才大庆式的这一道题
他其实还有个第三问
但是第三问比第二问
要更加的简单一些
这个二次函数还是刚才的二次函数啊
过的点是00和40
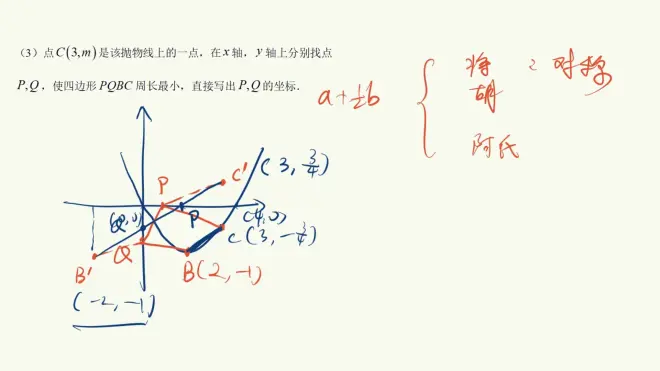
好然后他又新加入了一个点是3
那这个时候我就直接告诉大家了
c点的横坐标为3
由刚才的解析式可以得到
它的重指标是负的3/4
b点是什么
b点是这个二次函数的下顶点
那么b点的坐标当然就是2-1了
然后题目说
在x轴在y轴上分别找一个点p和q
使得周长最小
什么意思呢
比方说我p找在了这
然后我的q找在了这我随便点两个点
那么他给出来这个四边形就是p q b c
这个周长什么时候最小呢
涉及到折线段之和最小的问题除
了几何中的那些旋转之类的方法
或者说代数是求值
我们往往会考虑三大最值模型
第一大如果他是没有系数的
就像这样单独的加法
那么考虑的是将军一马模型
第二点如果他是带有系数的
比方说是a加1/2 b
我们考虑的是胡不归的方法
第三点如果他
得到的题目条件是
线段之间的比值一定的
那我们往往考虑的是20元的方法
三个思路去做
那么这道题是最简单的将军一马模型
将军一马模型的核心思路就是对称
我们只要把定点
关于动点的运动轨迹给对称开
答案就会自动的出来了
这句话啥意思
这里是不是一个定点c
那么这个点p它的运动轨迹是什么
是x轴那我们就
把这个点c
关于这个运动轨迹
做一个对称点就行了
做个对称点c一撇有什么效果呢
那么p c是不是永远等于p c一撇啊
同理嘛点q它在y轴上面运动
我们是不是可以过b
做这个y轴的一个对称点啊
那么对称点设为B一撇
那么b q是不是一定等于b q b撇q啊
我们是不是又把它对称走了
那我们再来看看
要求的这三个线段之和
是不是就变为了这三个线段之和
那为什么不理b c呢
因为b c是个动定值嘛
你永远不需要去考虑它
另外3个最小就行了
那么这三个线段之和什么时候最
短呀现在小学生都会了
你把这个一连吧
你把这个一连这就是周长啊
他加他是等于周长的最小值
那么p和q的坐标是不是就出来了
由于对称嘛
c点c撇的坐标是多少
c点坐标是他
那么c撇的横坐标不变纵坐标3/4
那么b点b撇呢
横坐标互为相反数
这是2这里就是-2纵坐标不变还是-1
所以我们利用这两个点的坐标
写出直线方程
再看看与x
y轴的焦点p q是不是就做出来了
这是我们说的最值模型
那考来考去反正总是这些东西嘛
那么与特殊图形的东西
就说的特别多了
我在之前里面也讲的非常的详细
所以说我给一个链接在旁边
大家手机的话就可以看到链接
直接点进
看看那个视频里面是如何讲的
各种特殊图形怎么去做
那么本节课为大家复习了一下
各种二次函数的性质与考伐
希望有所收获再见


