郑涛（Tao Steven Zheng）著

【问题】

奥玛·哈雅姆 （Omar Khayyam，1048 年 – 1131 年）通过把解形式为 的三次方程的问题转化为找出圆和抛物线之交点的问题：

其中   是正数。

题一： 推得 和 的关系。

题二： 通过绘制两个圆锥曲线并定位交点，用哈雅姆的方法求解三次方程 。

【题解】

题一解
把第一个方程写成 ，把第二个方程写成 。将第二个方程代入第一个方程来消除 ，得 。

因此，

或

与三次方程 匹配项，得

因为 都是正数，

题二解
对于方程 ， 和 。所以，

然后绘制两个圆锥曲线（二元二次方程）

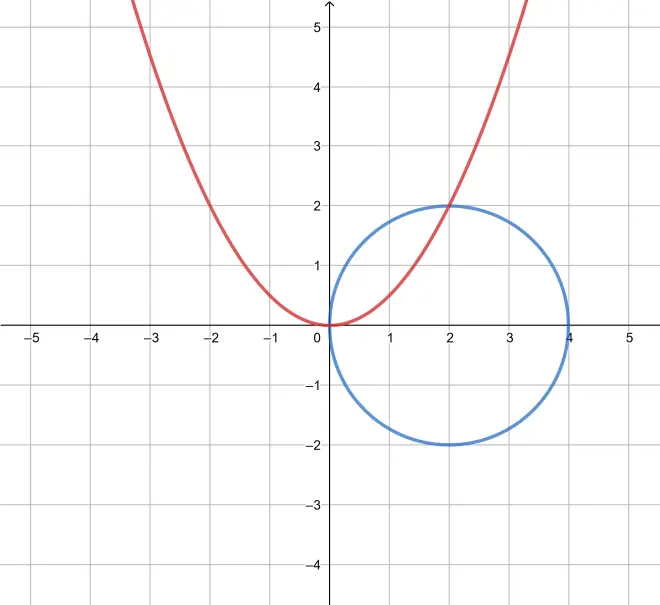
以上图所示，交点为 (0,0) 和 (2,2)。把这两个交点的 数值代入 时， 我们发现 此三次方程只有一个解 。