『数学』最值例题精讲5兼几何难题精讲3——加权费马点

2023-06-08 14:33 作者:Unfair-sany 0人读过 | 我要投稿

传送门:

上期传送门:『数学』点的存在性问题4:直角三角形＆二次函数例题精讲1(余式定理)
『几何』系列传送门:

第一期:几何难题精讲1(隐圆)

第二期:几何难题精讲2(瓜豆＆胡不归)

第三期:几何例题精讲1("12345"模型)

第四期:几何难题精讲3(加权费马点)(你所在的位置)
『最值』系列传送门:

第一期:费马点

第二期:阿氏圆1

第三期:阿氏圆2(隐圆)

第四期:二次函数周长最值

第五期:加权费马点(你现在所在的位置)

感觉标题用"兼"这个字比用符号"＆"看起来舒服多了呢(确信)

读前须知:

本期内容较多,请准备好大脑及阅读长篇废话(大嘘)的准备.

正文:

凭我的一丁点经验来看,阿氏圆和加权费马点虽然在数学考试中考的频率不高,但是一旦考了它,可以说在两个小时的考试中基本上是很难做完它的.

于是,这一期专栏就是为了解决这个问题而诞生.中考在即,而我在高考假专门抽出时间更新这样一期专栏就是希望能帮各位中考生们最后一把,毕竟,中考是能多得一分是一分的性质的考试,所以现在我也是能帮一点是一点,能多帮一个中考生是一个.

不多废话了,让咱们来看今天的例题吧.

一.例题

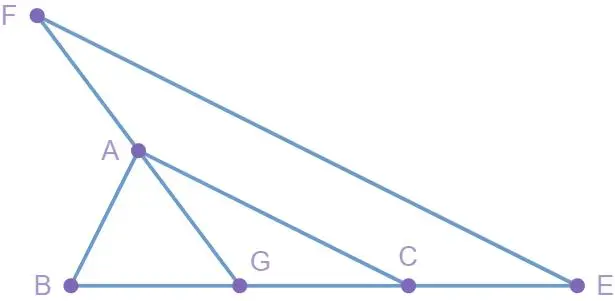
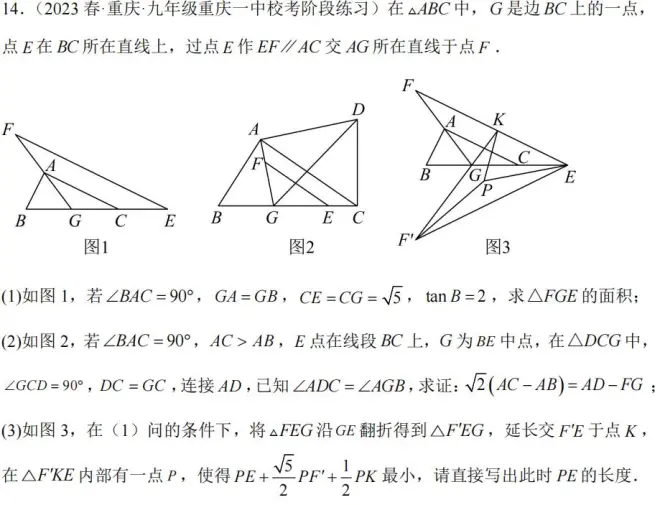
例1.(2023重庆一中阶段练习)在△ABC中,G是边BC上一点,点E在BC所在直线上,过点E作EF平行于AC交AG所在直线于点F.

(1)如图1,若∠BAC=90°,GA=GB, $CE%3DCG%3D%5Csqrt%7B5%7D%20$ ,tanB=2,求△FGE的面积;

(2)如图2,若∠BAC=90°,AC>AB,E在线段BC上,G为BE中点,在△DCG中,∠GCD=90°,DC=GC,连接AD,已知∠ADC=∠AGB,求证: $%5Csqrt%7B2%7D(AC-AB)%3DAD-FG$ ;

(3)如图3,在(1)问的条件下,将△FEG沿GE翻折得到△F'EG,延长F'G交FE于点K,在△F'KE内部有一点P,使得 $PE%2B%5Cfrac%7B%5Csqrt%7B5%7D%7D%7B2%7D%20PF'%2B%5Cfrac%7B1%7D%7B2%7D%20PK$ 最小,请直接写出此时PE的长度.

(注意:此处为第一个例题,第二个例题在学了通法之后用于实践兼秒杀(bushi))

((2)问特有的答辩解析)

看完题干之后,我们马上进入讲解.

二.讲解

(1)问没有什么好说的,面积为8.

在讲解(2)问之前呢,我们可以先欣赏一下网上的答辩解析.

反正我是没看懂它(悲.此处顺便口嗨一下,你说那个参考答案的解析为什么就不能写得简单一些(就像我马上讲的那个做法一样),写个让人如此 $FeSO_4$ (匪夷所思)的做法,搞得自己以为自己写的答案很高大上,其实就是依托答辩罢了.

那么我们回归正轨,继续讲题哈.

我们先对图形进行分析,是不是因为∠ADC=∠AGB,就有A,C,D,G四点共圆呢?是的呀,为什么呢?因为若四边形的一角的外角等于其内对角,即四边形对角加起来为180°,这个四边形便内接于一圆内,对吧?

又∠GCD=90°,DC=GC,那么△CDG就是等腰Rt△,就有∠CGD=∠CDG=45°.

又由圆周角定理,可得∠GAC=∠DAC=45°,亦可得∠BAG=90°-∠GAC=45°.

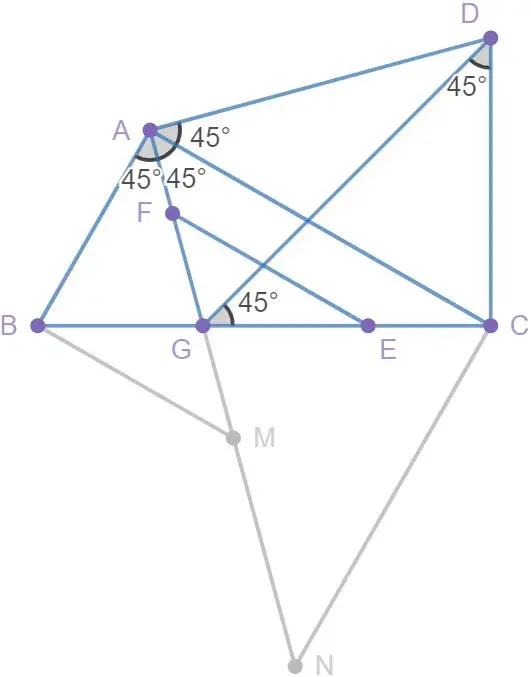
那么这时找 $%5Csqrt%7B2%7D%20AB%E5%92%8C%5Csqrt%7B2%7D%20AC$ 不就简单至极了吗?过B作 $BM%5Cbot%20AB$ 于B交AG延长线于M,过C作 $CN%5Cbot%20AC$ 于C交AG延长线于N.如图4.

就有 $AM%3D%5Csqrt%7B2%7DAB%2CAN%3D%5Csqrt%7B2%7DAC%5CRightarrow%20MN%3D%5Csqrt%7B2%7D(AC-AB)$ .

并且呢,这样作辅助线还有一个好处,就是图中出现了两组全等.

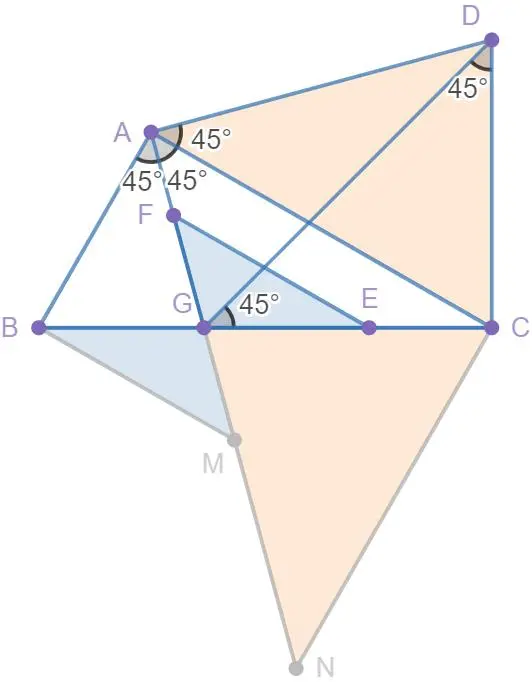
如图5,图中相同颜色的三角形是全等的.

此处简单讲解一下这些全等是怎么证明的.

易证BM平行于AC和EF,又BG=GE,便一定有 $%E2%96%B3BGM%5Ccong%20%E2%96%B3EGF$ .

而△DCG和△ACN都是等腰Rt△,所以根据"手拉手"模型,有 $%E2%96%B3DCA%5Ccong%20%E2%96%B3GCN$ .

于是FG=GM,AD=GN $%5CRightarrow%20$ MN=GN-GM=AD-FG.

综上,该结论成立.

(3)问的题型就是加权费马点,它看起来是要比普通费马点和上次那个费马点题目(详情见此处)难多了.我们还是先看一下它的解析在来进行讲解.

可以看出,加权费马点的本质还是旋转放缩(普通费马点不放缩或放缩比为1罢了).

那么我这边给出一个比较简单的做法.

如图6,将△PKF'绕点F'逆时针旋转90°至△P'K'F'处,以点F'为位似中心,1:2为位似比将△P'K'F'缩小成△P''K''F',连接PP''.

(这这这...你确定这个叫简单做法?还不是要做这么多辅助线.)

可以得到 $P''K''%3D%5Cfrac%7B1%7D%7B2%7DPK%2CPP''%3D%5Cfrac%7B%5Csqrt%7B5%7D%7D%7B2%7DPF'$ ,即原式转换为EP+PP''+P''K''.

根据"两点之间直线段最短",有原式的最小值为EK''.

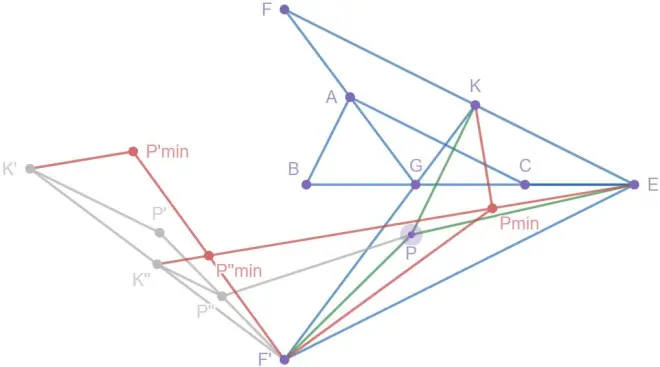
此时,我们找到了最小值,那么我们应该怎么去求EP长呢?此时我们就要用(1)里面没用的长度和角度条件了.

由tanB=2,我们便令∠ACB=α,可得tanα=½(懂得都懂),∠KEF'=2α,∠KF'E=α.

由"12345"模型可得 $tan2%CE%B1%3D%5Cfrac%7B4%7D%7B3%7D$ .(不懂看这里)

又由 $CE%3DCG%3D%5Csqrt%7B5%7D$ ,可得AB=2,AC=4,EF=EF'=8.

必然的,已知两角和一边解三角形,我们现阶段必须要作垂线才可以解决它.

所以我们过点K作 $KD%5Cbot%20EF'$ 于D. 如图8

我们设KD=4a,则DF'=8a,ED=3a,可得11a=8,即 $a%3D%5Cfrac%7B11%7D%7B8%7D%20$ .

所以 $KD%3D%5Cfrac%7B32%7D%7B11%7D%2CDF'%3D%5Cfrac%7B64%7D%7B11%7D%2CED%3D%5Cfrac%7B24%7D%7B11%7D$ .

由勾股定理可得 $KF'%3D%5Cfrac%7B32%5Csqrt%7B5%7D%7D%7B11%7D%2CKE%3D%5Cfrac%7B40%7D%7B11%7D$ .

又tan∠P''minPminF=½,所以∠P''minPminF=α.

由外角可知∠K''P''minF'=∠K'P'minF'=90°+α.

由旋转可知∠KPminF'=90°+α,可得∠KPminE=90°.

别忘了题干,我们要求的是EPmin的长度,而在几何题里要求长度,现阶段只能用相似或着解三角形才可以.

所以我们连接KK'',过E作 $EH%5Cbot%20KK''$ 于H.如图9

易得∠F'KK''=α,可证得KH平行于DE.

可解得 $KK''%3D%5Cfrac%7B80%7D%7B11%7D%2CEH%3DDK%3D%5Cfrac%7B32%7D%7B11%7D%2CKH%3DDE%3D%5Cfrac%7B24%7D%7B11%7D$ .

于是 $HK''%3D%5Cfrac%7B104%7D%7B11%7D%2CEK''%3D%5Cfrac%7B8%5Csqrt%7B185%7D%7D%7B11%7D$ .

又由△PminKK''∽△HEK'',有 $%5Cfrac%7BEK''%7D%7BKK''%7D%3D%5Cfrac%7BHE%7D%7BKP_%7Bmin%7D%7D%2C%E5%8D%B3%5Cfrac%7B%5Cfrac%7B8%5Csqrt%7B185%7D%7D%7B11%7D%7D%7B%5Cfrac%7B80%7D%7B11%7D%7D%3D%5Cfrac%7B%5Cfrac%7B32%7D%7B11%7D%7D%7BKP_%7Bmin%7D%7D$ .

解得 $KP_%7Bmin%7D%3D%5Cfrac%7B64%5Csqrt%7B185%7D%7D%7B407%7D$ .

在Rt△EKPmin中,由勾股定理可得: $EP_%7Bmin%7D%3D%5Csqrt%7B(%5Cfrac%7B40%7D%7B11%7D)%5E2-(%5Cfrac%7B64%5Csqrt%7B185%7D%7D%7B407%7D)%5E2%7D%20%3D%5Cfrac%7B8%5Csqrt%7B185%7D%7D%7B37%7D$

终于把这个既难想又难算的题做完了\(^o^)/~,但这明显不是这一期的末尾.

三.方法讲解:加权费马点

在真正讲解它之前,我先讲一下余弦定理和托勒密不等式,因为讲解通法时要用.而且例2由于篇幅原因,就只呈现(3)问力(悲,多好的一个题啊).

首先是大家应该不陌生的余弦定理,它描述的是任意三角形中的边角关系.对于△ABC,若∠A、∠B、∠C的对边分别为a、b、c,则有如下关系式成立:

a²=b²+c²-2bccosA b²=a²+c²-2accosB c²=a²+b²-2abcosC

特别地,在直角三角形中,该定理退化为勾股定理,即a²=b²+c².

此处只证明当三角形为锐角三角形时余弦定理是否成立.

如图10,在锐角△ABC中,过A作 $AD%5Cbot%20BC$ 于D.

于是c²=AD²+BD²=b²-DC²+(a²-DC²)=a²+b²-2a·DC=a²+b²-2abcosC,即c²=a²+b²-2abcosC成立.同理可证得其余的等式成立.

钝角三角形我们不予证明,你只需要知道cos(180°-α)=-cosα即可.

然后就是余弦定理的推论了,该推论反映了三角形已知三边求角的方式:

$cosA%3D%5Cfrac%7Bb%5E2%2Bc%5E2-a%5E2%7D%7B2bc%7D%2CcosB%3D%5Cfrac%7Ba%5E2%2Bc%5E2-b%5E2%7D%7B2ac%7D%2CcosC%3D%5Cfrac%7Ba%5E2%2Bb%5E2-c%5E2%7D%7B2ab%7D$

余弦定理及其推论也可证明为什么满足SSS和SAS的两个三角形全等的问题.

接下来就是大家不太熟悉的托勒密不等式了,此处只证明托勒密定理,而托勒密不等式大家可以自行去证明.

托勒密定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积;而托勒密不等式说的是:凸四边形的两组对边乘积和不小于其对角线的乘积,当且仅当共圆或共线时不等式可取等号(由于共线的情况基本上可以排除,所以下文运用该不等式说明取等条件时就只会说共圆).接下来我们就来证明托勒密定理.

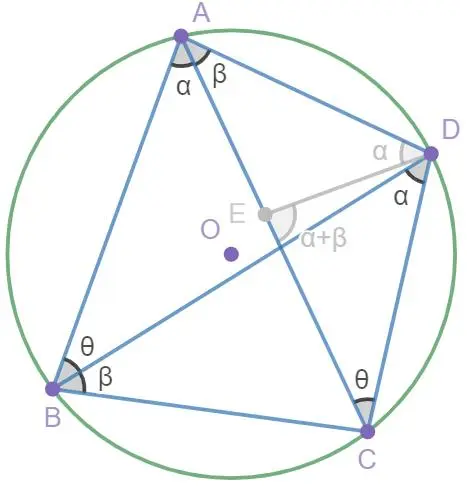
如图11，四边形ABCD内接于圆O内,现在我们要证明的是AC·BD=AB·CD+AD·BC.我们便在AC边上取一点E,使∠ADE=∠BCD,连接DE.

这样做的话就会有△ADF∽△BDC和△ABD∽△FCD,可得 $%5Cfrac%7BAD%7D%7BBD%7D%3D%5Cfrac%7BAF%7D%7BBC%7D%2C%5Cfrac%7BAB%7D%7BFC%7D%3D%5Cfrac%7BBD%7D%7BCD%7D$ ,即AD·BC=AF·BD,AB·CD=BD·FC.

两式相加,可得AB·CD+AD·BC=BD·(AF+FC)=AC·BD.于是我们便证明了托勒密定理成立.

同学们可以用同样的方式证明托勒密不等式.

接下来,我们就对加权费马点进行讲解了.

首先,我们先把旋转放缩法给讲了.

要想讲明白加权费马点,首先我们得需要知道加权费马点的一般题干是什么.一般来说,它的题干是这样子的:

已知△ABC,P为△ABC内部一点(含边界),求aPA+bPB+cPC(a,b,c均为正实数)的最小值.

题目中还有其他的用于解题的条件,此处略去.

由于该题目中a,b,c的组合太多,所以该题要分四种情况进行讲解.

①当a=b=c=1时,即三边均不加权或三边加权系数相同时:

此时该题目就是一般费马点,你可以看往期我对它的讲解(看这里),或着在这里听我逼逼赖赖(bushi).

对于这种题,我们只需要将任意一个含点P的三角形绕原三角形的任意一个顶点向远离原三角形的方向旋转60°,如图12

这个时候我们还需要分类讨论一下.

(i)当∠A,∠B,∠C均小于120°时:

这时怎么做就不用我教了吧(主要是篇幅原因和图片数量原因的限制就不讲了),不知道的话去看往期吧.

此时取到最小值的P有如下性质:满足∠APB=∠BPC=∠APC=120°,这也是为什么会出现下一个情况的原因.

(ii)当∠A,∠B,∠C中有一个角大于等于120°时:

此时点P在原三角形外了(悲),那么这个时候的最小值就在钝角顶点处取最小值,其为该钝角的邻边长度之和.

记得当三边加权系数相同时要先提取系数出来,最后写最小值时要乘提取的系数哦!

②当a,b,c中有一个数不为1,即一边加权时:

不妨设b为非1系数,旋转角度为α(0°<α≤180°),则旋转中心应为所加权的系数对应的加权线段而所对应的原三角形的顶点,此处b所对应的加权线段为PB,则旋转中心为点B.

如图13即为刚刚讲解的情况.

仔细看这个图,你知道b和α之间满足的关系了吗?

没错!要想让PP'=bPB,只需要sin½α=½b即可.

但是由于sin½α的值域为[-1,1],取正数的话就是(0,1],那么此时我们又要分情况讨论了.

(i)当sin½α>1,即b>2时:

此时看似无解(毕竟此时的角度不是实数角度了对吧),也就是无法旋转了是吧?那么就分析一下,是不是PB对这一坨式子的值的变化影响最大(毕竟它加权了嘛),那么我们让加权边为0时是不是就回让它们的和最小了呢?

那么这种情况的最小值就是旋转中心的邻边之和.

(ii)当sin½α=1,即b=2时:

可得α=180°,这时和倍长中线没什么区别.

此处用变化率来描述的话(也就是(i)的方式)也可以,但我觉得还是看了(iii)(iv)之后再说.

(iii)当∠B<180°-α时:

为什么这个情况下会给∠B这样一个限制条件呢?我们马上讲.

在此情况下,当C,P,P',A'四点共线,即上述式子取到最小值时,有∠APB=∠BPC=90°+½α,即可得∠APC=180°-α.

可以看出,在此条件下点P是不可能跑出△ABC的,那么此时的最值就在△ABC内部取到,而不是某一个顶点上.

(vi)当∠B≥180°-α时:

此时构成最小值的P跑到△ABC外部去了,所以此时的最值在点B处取到,其值为该角的邻边之和.

那么对于(ii)的情况说,因为∠B恒大于0°,所以说(ii)的情况只能在点B处取到最值.

③当a,b,c中有两个数不为1,即两边加权时:

这种情况应该就是最难的一种情况了.

不妨设a,c为非1系数且a<b<c(若a=c则可以通过提取系数的方法变为②的情况了),旋转角度为α(0°<α≤180°).

此时满足 $cos%CE%B1%3D%5Cfrac%7Ba%5E2%2Bb%5E2-c%5E2%7D%7B2ab%7D$ (the law of cosine的推论:像啊,很像啊(喜)),即旋转角的余弦值等于三边系数中两个较小的系数的平方之和减去较大系数的平方的差除以二倍两个较小系数的乘积之商的值(看着还挺复杂的,但其实你知道余弦定理的推论就比较简单了).

那么为什么cosα会满足这个式子呢?我们马上就简单证明一下.

假定它能在原三角形内部取到最小值,那么我们就以最大加权边所对应的原三角形的顶点为旋转中心,在该情况下即为点C,像远离原三角形的方向旋转.然后将旋转过后的三角形以第二大加权系数为位似比,刚刚的旋转中心为位似中心进行位似变化,此处为a为位似比,P为位似中心(注意哦,第二大加权系数不是b是a哦,因为b=1,对于PB而言不是加权).

那么PP''²=PC²+P''C²-2PC·P''Ccosα= $PC%5E2%2Ba%5E2PC%5E2-2aPC%5E2%C2%B7%5Cfrac%7Ba%5E2%2Bb%5E2-c%5E2%7D%7B2ab%7D$

由b=1可得PP''²=PC²(1²+a²-a²-1²+c²)=c²PC²,即PP''=cPC.

而且我们还可以证明到:当原式取到最小值时,由∠A''P''C+∠BPC=∠APB+∠BPC=180°+α,可继续推得∠APC=180°-α.

这时,由于cosine funtion的值域和三角形的形状问题,我们又会分种情况讨论:

(i)当cosα≥1或cosα<-1时:

这时看似又无解了是吧?因为此时的角度是复数角,你不会旋转啊!那么这个时候我们怎么办呢?如果还是考虑变化率的话,应该是可以的,那么此时的最小值就是在旋转中心处取到最小值,为aAC+BC.

(ii)当cosα=-1时:

这个情况与②(ii)的过程和结果相同,我们就不过多讲解了.

(iii)当∠C<180°-α

可以看出,在此条件下点P也是不可能跑出△ABC的,那么此时的最值就在△ABC内部取到,而不是某一个顶点上.

(iv)当∠C≥180°-α

同样的,此时构成最小值的P跑到△ABC外部去了,所以此时的最值在点C处取到,其值为aAC+BC的值.

④当a,b,c均不为1,即三边加权时:

此时不妨设a>b>c.

这个情况就简单多了,我们只需要提取中间大的系数b,那么此时的式子就转换为形如 $b(%5Cfrac%7Ba%7D%7Bb%7DPA%2BPB%2B%5Cfrac%7Bc%7D%7Bb%7DPC)$ 的式子,也就是③的类型了,那么之后就是该怎么解就怎么解.

当然,你想提取其他系数也可以,只不过就是做起来复不复杂的问题了,提取中间大的系数相对简单一些.还有,求到最小值的时候要检查自己乘了系数没有!

接下来,就是非常好用的托勒密不等式法了(坏笑).

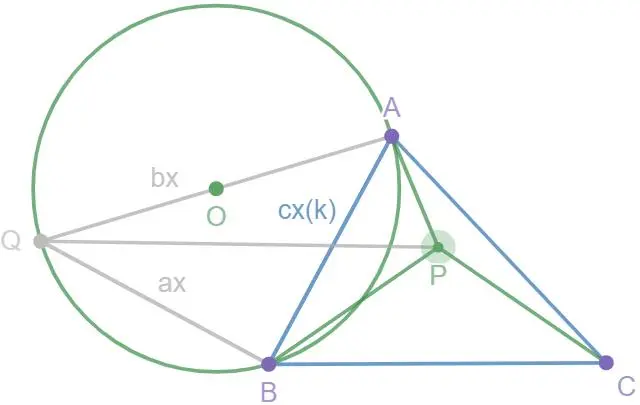
如图15,我们以三角形任意一边向外构造一个三角形,使A、B、P、Q这四点可以构成四边形.还要满足AP的对边QB=ax(x为任意正实数),BP的对边AQ=bx,还有AC=cx.为什么要这样构造三角形呢?因为根据托勒密不等式,有AP·BQ+BP·AQ≥PQ·cx(当且仅当A,B,P,Q四点共圆时等号成立),即AP·ax+BP·bx≥PQ·cx,aAP+bBP≥cPQ(当且仅当A,B,P,Q四点共圆时等号成立).

此时不等式两边同加cPC,有aAP+bBP+cPC≥c(PQ+PC)(当且仅当A,B,P,Q四点共圆时等号成立),而PQ+PC≥CQ(当且仅当C,P,Q三点共线时等号成立),也就是aAP+bBP+cPC≥cCQ(当且仅当A,B,P,Q四点共圆且C,P,Q三点共线时等号成立).同时也证明了,对于一个确定的三角形ABC和加权系数a,b,c,我们可以找到唯一确定的点P,使得aPA+bPB+cPC的值最小.

但是,由于a,b,c可能构不成三角形,所以我们又要分两种情况讨论:

(i)当a,b,c构不成三角形时:

此时就无法使用托勒密不等式了(悲),但是你想一下,我们之前那些看似无解的情况,是不是和这个情况类似吗?比如当sin½α>1,即b>2时,是不是有a+c<b,即这三个系数构不成三角形,对吧?还有使余弦值不满足它的值域的三个加权系数,用余弦定理推断出不合理结果就是因为这三个系数构不成三角形,为什么这样说呢?因为余弦定理只在三角形内满足.

那么我们就可以知道,当a,b,c构不成三角形时,根据变化率的影响,我们可以得知,当点P与最大加权系数重合时,就取得最小值了.

(ii)当a,b,c构成三角形时:

此时就接着刚刚的分析过程,该怎么做就怎么做,我就不做过多讲解了.

四.实战

让我们再用一个例题来巩固一下刚刚讲过的题目.

例2.如图,△ABC为等边三角形,点D为AC边上一动点,连接BD,将线段BD绕点B逆时针旋转角α得线段BE.

(3)如图16,若α=120°,将△BDE沿BD翻折得△BDE',M为AB中点,连接ME',当ME'最小时,在△BCD内找一点P,使 $%5Csqrt%7B3%7DPB%2B2PD%2B%5Csqrt%7B7%7DPC$ 的值最小,若BC=4,直接写出其最小值.

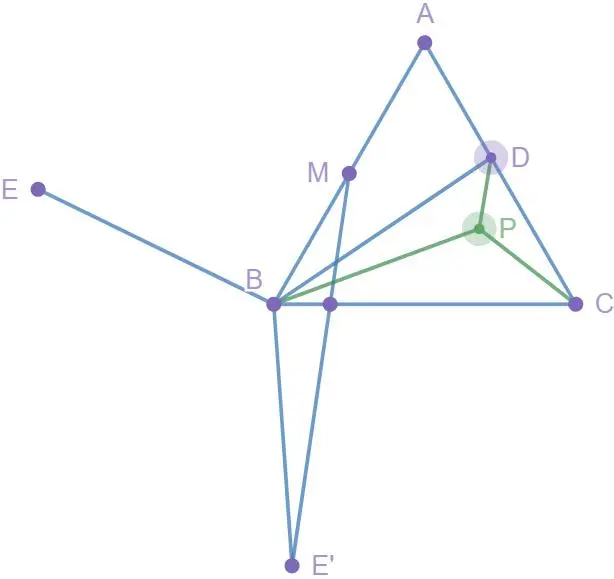
根据瓜豆易得E,E'在一条定线段上运动,但具体是哪条线段呢?

如图17,我们作这三条垂线段,易证得全等,那么它的轨迹不就出来了吗?

根据"垂线段最短",可以得到ME'的最小值.此时G'E'=1=DF.

此时,我们隐藏去不需要的线段,原题目就转换为:

已知△DBC,∠C=60°,BC=4,DC=3,求原式的最小值.

此处我们两种方法都用一下.

①旋转放缩法

我们将△BPC绕点C逆时针旋转90°至△B'P'C处,以点C为位似中心, $%5Cfrac%7B%5Csqrt%7B3%7D%7D%7B2%7D$ 为位似比缩小△B'P'C至△B''P''C,连接PP''.如图18

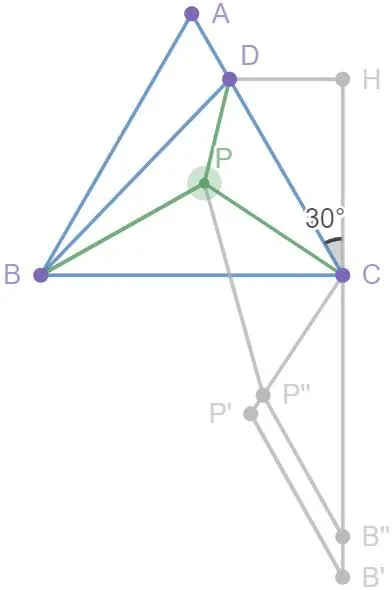
于是 $%5Cfrac%7B%5Csqrt%7B2%7D%7D%7B2%7DPB%3DP''B''%2C%5Cfrac%7B%5Csqrt%7B7%7D%7D%7B2%7DPC%3DPP''$ ,则原式转换为求2(DP+PP''+P''B'')的最小值,这个就很简单了.

当D,P,P'',B''四点共线时,2(DP+PP''+P''B'')min=2DB'',此处过D作 $DH%5Cbot%20CB''$ 于H.

易得 $DH%3D%5Cfrac%7B3%7D%7B2%7D%2CCH%3D%5Cfrac%7B3%5Csqrt%7B3%7D%7D%7B2%7D%5CRightarrow%20HB''%3D%5Cfrac%7B7%5Csqrt%7B3%7D%7D%7B2%7D%2CDB''%3D%5Csqrt%7B39%7D$ .

那么原式的最小值就是 $2%5Csqrt%7B39%7D$ .

②托勒密不等式法

我们便以BC为一边向△DBC外部构造△BCQ,满足 $BC%3ACQ%3ABQ%3D2%3A%5Csqrt%7B3%7D%3A%5Csqrt%7B7%7D$ ,连接PQ.如图19

由托勒密不等式可得 $%5Csqrt%7B3%7DPB%2B%5Csqrt%7B7%7DPC%5Cgeq%202PQ$ .

两边同加2PD,可有 $%5Csqrt%7B3%7DPB%2B2PD%2B%5Csqrt%7B7%7DPC%5Cgeq%202(DP%2BPQ)%5Cgeq%202DQ$ (当且仅当B,C,P,Q四点共圆且D,P,Q三点共线时等号同时成立).

那么原式的最小值就是2DQ了,求长度的过程是一样的,此处略去.

那么这个题就讲到这里了哦.

当然了,可能现在有些同学还是有一些懵,或着有些同学已经想要开始练练题了.对于前一部分同学,up主在这里先说一下,现在up正在赶加权费马点的文档资料了,所以呢这一部分同学只能先就这这一篇专栏看着.而后一部分的同学呢,我这边还有一套"几何压轴20题"的资料,如果有想要资料的同学可以加入up的粉丝群:105292396,或着私信up主获取哦!(＾Ｕ＾)ノ

此处爆出几何压轴20题的截图来证明我有这一套资料: