【最后十课】一小时拿下“解三角形“所有题型!2023高考冲刺!第3讲

解三角形?你一定行!一举成名?出奇制胜!
笔记总结 + 详细笔记 + 补充参考
记得比较全面,希望笔记能对你有所帮助
━━━━━━━━━━━━
●●●总结
你什么水平你自己知道,标题就是以押韵为主,都40天不到了,得现实一点
开头是所有三角函数公式总览
边角互化有方向,齐次、范围要注意
🔲1️⃣🔳1️⃣🔲4️⃣🔳🔲🔳🔲🔳🔲🔳🔲🔳🔲🔳🔲🔳🔲🔳🔲🔳🔲5️⃣🔳1️⃣🔲4️⃣🔳
公式一览,有几个跟本节关系不大,就当给自己看了:


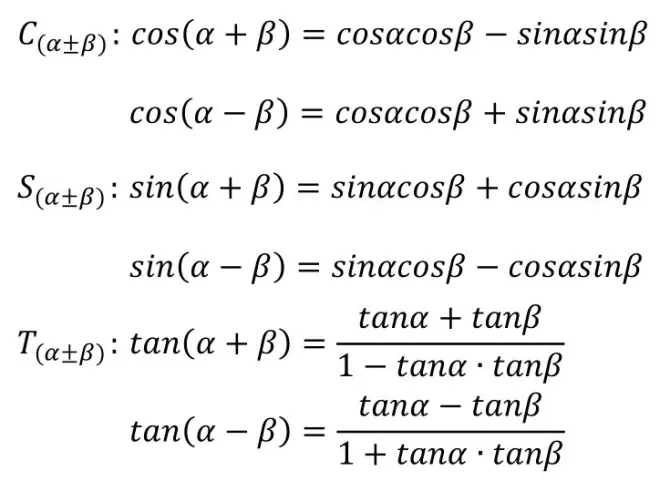

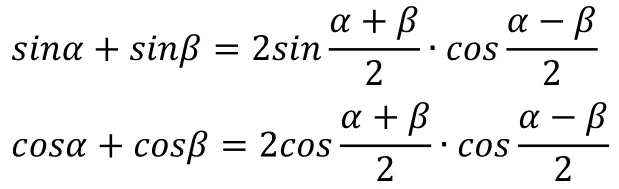
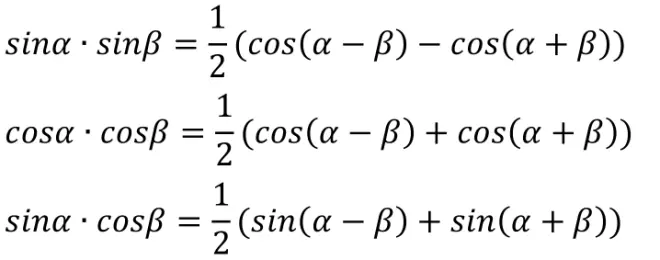





📀1️⃣ 正弦定理简单应用
→何时使用正弦定理和余弦定理
- 角度转化:三角形内角和为π,可利用三角函数中的角度转化,两角表示一角,换元化简
- 余弦定理:一角三边;平方和、边之积或和;完全平方;基本不等式
- 正弦定理:两对边对角;边角转化(等号左右齐次);涉及外接圆

识条件:不是对边对角,有两边极其夹角,用余弦定理;
得第三边c,再次利用余弦定理

i 识条件:已知两角一边,求∠C的对边长
直接正弦,得BD长
ii 识条件:要求∠ABD,可以利用∠DBC得到
已知另两条边,用三角函数中角度转化
📀2️⃣ 边角等式化简
化简要有方向性,不要当无头苍蝇:
确定是角化角,还是边化角、角化边、边化边;用正弦定理就要注意齐次
⚛️角化角

i 化简就要统一角的倍数,把A/2转化为A,最容易想到的是倍角公式

ii 齐次了,交叉相乘不影响化简,同时得到cosAcosB-sinAsinB,可以直接化简
⚛️边角互化
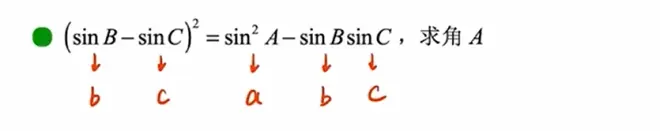
齐次+余弦定理得角A
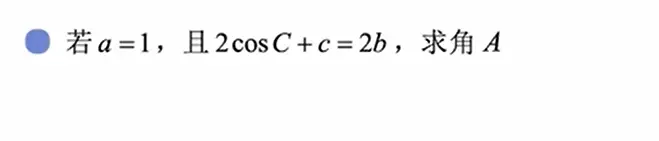
i 利用a=1,使等式左右都有边(齐次),利用正弦定理进行边化角
ii 2cosA=1 直接得A

i S△ABC=1/2*b*c*sinA可得左式有b*c,右式有a²,边的齐次,边化角消sin²A
ii cosB*cosC-sinB*sinC=cos(B+C)→cosA
⚛️边化边
因式分解
⚛️练习题

📀3️⃣ 最值、范围问题
- 化成角:余弦定理+基本不等式
- 化成角:正弦定理+三角函数
→消元



i 根据已知,要利用∠B,用余弦定理
ii 化简,得ac=a²+c²-b²,S△ABC=ac*(根号三/4),发现只用上了a、c
iii 既然要求ac范围,就利用b=10-a-c换元化简保留a、c
iv ac<100,确定ac最大值,得S△ABC最大值


i 边化角
ii A+B+C=π,C=2A→sinB=sin3A
iii 三倍角化为二倍角+一倍,化简,但是不先化cos2A,看情况随机应变
iv 基本不等式/对勾函数


i 角化边,消去多余角C,
ii 锐角,则A∈(π/6,π/2)
📀4️⃣ 解多三角形
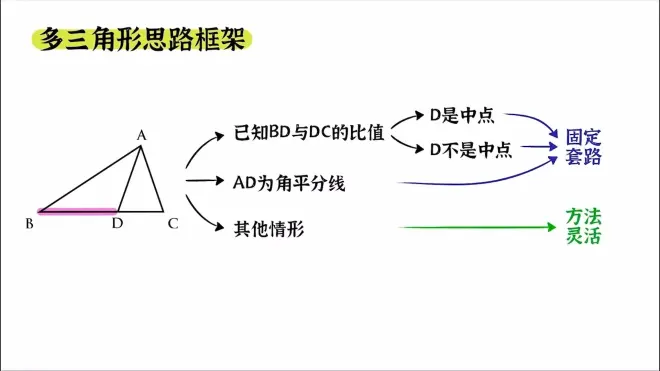
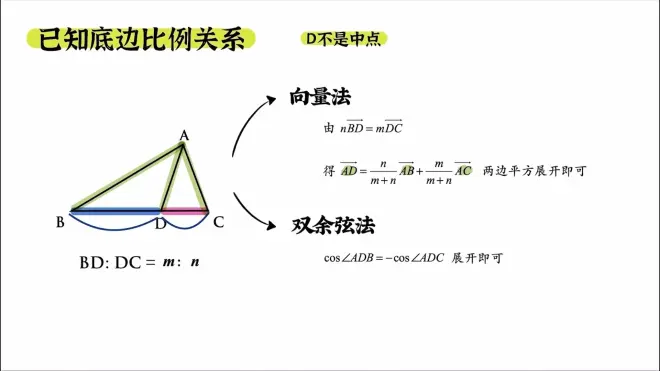
⚛️ 已知底边比例关系
- 向量法(利用角):特殊点的,当点为中点时即为极化恒等式
联系AD、AB、AC和∠BAC
- 双余弦法(全是边的关系):利用互补的两个角和余弦定理
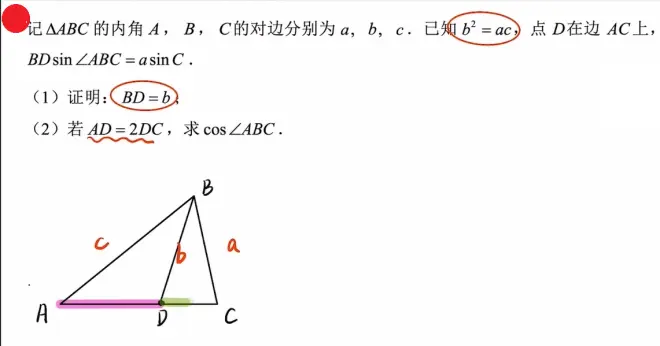
(2)
i 不知角的关系,用双余弦法
ii 化简,得3c²+6a²-11b²=0 消去b
iii 检验,将a/c代入cos∠ABC,得结果
⚛️ 角分线模型

⚛️ 其他类型条件
由特殊到一般:
三个三角形组成,利用互补的两个角联系两个小三角形

i 怎么才能联系到互补的∠ADC和∠BDC,涉及两个角,利用正弦定理
ii 得到x与y的关系式,再利用∠BCD的余弦定理,得到x与y的方程
iii 双余弦模型:x²+y²=2(AD²+BD²)=6
iv 解一元三次方程,先试出一个解,再因式分解

●●●补充参考
开头的公式图片自己收集麻烦,皆来自于微信公众号文章,作者为 素人素言 ,写高中数学各大专题内容都的挺有意思
victory!!
对了,统一一下意见,各位有没有对笔记原文件的需求,我会把“高考系统课”的笔记像奇哥一样放到云盘中供大家免费食用,如有需求可以私信、评论来告诉我 (笔记格式是PDF格式,使之不漏标记,并且我还进行了精简,还把整体颜色加深满足打印的需求)


