《高等代数》全程教学视频(宋浩老师)

个人笔记
2.2 排列

1.排列是有序数值 中间不能缺 1245不是排列
2.逆序数如何计算:标箭头 然后数有几个数字比6小 有五个 以此类推相加。如果有奇数个 就是奇排列 反之偶排列。
2.3 n阶行列式

n=4k+1或者4k时为偶排列
n=4k+2或+3时是奇排列


行列式形状是方的 用直线
矩阵用()和 [ ]


主对角线全是正 副对角线考虑正负
2.4 行列式的性质
转置行列式就是把原始的行变成列 列变成行
性质一:转置行列式与原行列式相等
性质二:交换行列式的两行 要变号
推论:行列式中 两行(列)相等 D=0
性质三:用k去乘行列式的某一行元素等于用k去乘行列式
推论一:D中有一行的元素都有公因子k k往外提一次,D中所有元素都有公因子k往外提n次推论二:D中两行成比例 D=0
性质四:见下图(例如 把一个行列式分成两个相加 第一行拆开后 其他行保持不变 不能全部都拆开)
性质五:将D的某一行(列)元素都乘以k 加到零一行上去 D值不变




2.6 行列式按一行(列)展开
1.余子式就是划个十 剩余的部分(M
代数余子式是在前头乘以(-1)的 角标和 次方(A

2.行列式按行(列)展开定理:
n阶行列式=它的某一行(列)的元素 与 其对应的代余子式的乘积之和

❗学会构造

(1)计算第一问的余子式与第四行是什么无关。原式子第四行有对应的余子式 第一问也有对应的余子式。那我们就构造第四行是1111即第一问的系数。可以看见右下角计算A21+A22 可以构造成1100
异乘变零定理(期末考得不多 考研多):某一行元素与另一行元素的代数余子式乘积之和=0

原理:前面提到的构造+行列式两行相等 行列式=0
2.8 拉普拉斯定理-行列式的乘法规则

2阶子式:两条杠交集的数字
余子式:剩下的
代数余子式(-1)的右上角:二三行三四列 然后相加
拉普拉斯定理(适用于有一块0的):在D中取定 k行 由这k行所组成的一切k阶子式与其代数余子式乘积之和=D(意思就是 先取定三行 然后再取三列 比如123列 124列 125列然后算出来相加)

2.7 克拉默法则 (缺点:计算量大)
定理:含有n个方程n个未知数的n元方程组 其系数行列式≠0时 x1=D1/D X2=D2/D Xn=Dn/D
(D1就是方程组最右边一列数取代D中第一列 D2D3同理)
条件:
①方程个数=未知数个数(因为要做成行列式 行列式是方的)
②D≠0(因为分母不可以为0)

齐次线性方程组:常数项全部为0的线性方程组
方程组如上 但是常数项全为0 方程组只有零解 (行列式只要有一行/列全是0 D=0)


①齐次方程组一定有解 至少有零解(解=0)
②齐次 方程个数=未知数个数 D≠0,只有零解(满足克莱姆法则 用右边一列0取代 分子上的 行列式对应列 解=0)
③齐次 方程个数=未知数个数
如果有非0解 D=0 /如果D=0 有非零解
(②的逆否命题 如果D≠0 怎么可能有非零解 应该只有零解)

2.5 行列式的计算1

( 1)

(2)爪形行列式解体技巧一样:用-2消掉1,-3消掉1,以此类推 (想办法化成上三角下三角)



(3)也可以直接把最后一行按行列式展开计算
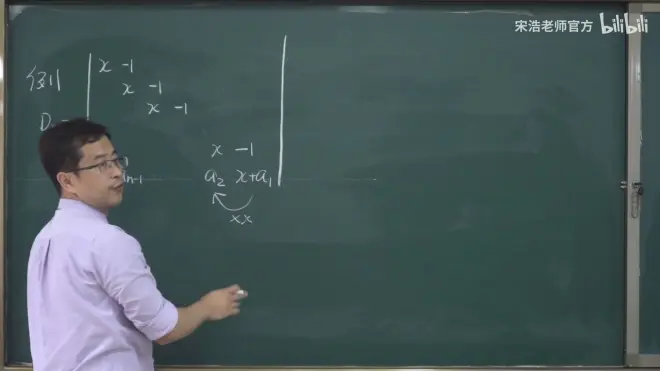

行列式计算2
(1)(2)都要用范德蒙(ps:范德蒙德在线代1.4)
(3)考研真题
①用拉普拉斯定理

②

行列式计算3
(1)加边法【用的少】+爪形

竖着看 说是因为X1 X1 X1/X2 X2 X2/XnXnXn 所以用加边法(加一行加一列的意思)

3.2 n维向量空间
【α=(a1a2...an) 其中a代表几维
α的行向量 通过转置就变成列向量了
(行矩阵和行向量一个意思 不过前者没有逗号)
问:两个零向量相等吗 答:不相等 维数不一定相同
向量的相等:同种的向量 每个分量都相等
eg:(a,b,c)=(1,2,3)】
线性运算:α是向量/矩阵 k是常数
AB=0推不出A=0或B=0(AB是矩阵 矩阵乘法三个不满足)

3.3 线性相关性
线性组合:k可以全是0 得到的不就是零向量

线性表示:
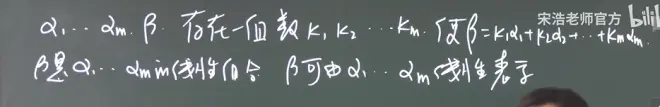
线性表示结论:

线性相关:k不全为0(找到一组就行)
线性无关:找不到k不全为0的情况

结论:

(3)(4)考研用得很多
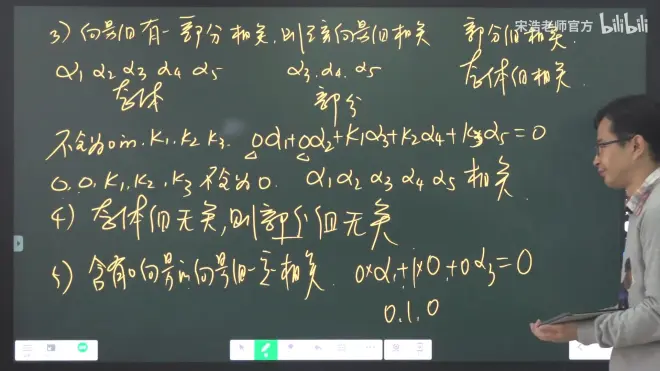

(8)线性无关的向量组的接长向量组也无关
线性相关的向量组的截短向量组也相关【少】
部分组相关 整体相关
整体无关 部分无关【多】
(9)向量组有两个向量组成比例 则该向量组相关
向量组的等价
矩阵的等价是 由A初等变换得到B,A等价于B
向量组的等价:(1)(2)可以相互线性表示
①反身性 ②对称性 ③传递性

p61先空着 好烦 不想看
极大无关组(所含向量个数最多的线性无关的部分组):a1 a2是向量组的部分组。①部分组无关【r个】②任一向量均可由部分组表示。
任【r+1】个向量都相关
结论:①零向量 没有极大无关组
②线性无关的向量组其极大无关组是本身
③向量组的极大无关组可能不唯一
④向量组与极大无关组是等价的
⑤向量组的两个极大无关组等价 且所含有向量个数相同
⑥ 向量组(1)可以由向量组(2) 表示 则1的极大无关组也可以由(2)的极大无关组表示
⑦等价的向量组 其极大无关组也等价(传递性)
求极大无关组
初等行(列)变换不改变矩阵列(行)向量的线性关系

↓要化成行简化

后面顺序乱掉了 有点找不到是第几节
4.2 矩阵的运算
矩阵的数乘
矩阵提取公因子:矩阵所有元素都有公因子k k往外提一次
行列式提公因子:一行有公因子k k往外提取一次,n行都有公因子k 提取n次
规律

矩阵的乘法
①矩阵列数等于矩阵行数
②结果矩阵(c)的行数等于第一个(a)的行数 列数等于第二个矩阵的列数(b)
中间相等取两头 就是c的格式
eg A2×3 B3×4 结果矩阵就是2×4
矩阵不相乘不满足什么
ab≠ba (b或者a是单位矩阵的时候可以相等
ac+bc=c(a+b)是错的 c应该在右边。
即=(a+b)c
结论:
(1)不满足交换律:① ab能相乘的时候ba不一定可以。毕竟要满足中间相等。
②即使ab ba都有意义 一般两个不相等
③如果ab=ba 叫做ab是可交换的
(2)不满足消去律:若AB=AC 且A≠0 推不出B=C。(矩阵=0可以是各种各样的)
但是A可逆的时候推得出 左右两边同乘A的-1次方 其积是单位矩阵 这时候B=C
(3)④两个非0矩阵的乘积可能是零矩阵(所以AB=0推不出A等于0或者B等于0.AB是矩阵)
但是B可逆的时候 可以推出A=0
矩阵相乘满足:
(1)结合律:(AB)C=A(BC)
(2)分配律:(A+B)C=AC+BC
(3)k(AB)=(kA)B=A(kB)
(4)AE=A , EA=A
(5)A*0矩阵=0矩阵 , 0矩阵*A=0矩阵
(6)1*A=A ,0数字*A=0矩阵
(7)A=aE AB=aEB=aB
(8)对角型✖对角型=对角型(就主对角线有数字 相应数字相乘)
矩阵的初等变换
行/列:①交换两行 ②非0数乘以某一行 矩阵不变行列式变 ③某一行的l倍加到另一行上去
矩阵的标准型(任意矩阵都有标准型 可以不是方阵):除了最上面那个 其他被杠掉的都不是标准型。标准型左上角就得是1 斜着连续的1。像第二行第二个全是0也可以。

伴随矩阵
①只有方阵有 但不是所有的方阵都有伴随矩阵
②按行求 按列放。(记得是代数余子式的转置
性质
①AA✳=A✳A等于|A|E


