信号的不确定性原理

    信号的不确定性原理，也就是量子力学里的海森堡测不准原理。它指出：信号的时宽和频宽不可能同时任意地窄，这也就意味着，不可能通过任何方法上的改进同时得到完全精确的信号时间、频率信息。当使用短时窗进行傅里叶变换，信号的时间信息变得精确，同时频率信息变得不精确；当使用长时窗进行傅里叶变换，信号的频率信息变得精确，同时时间分布信息变得不精确，因为你得到的频率信息是分布在整个时窗中的。

    因此，之后介绍的任何方法，都受制于不确定性原理。

为了说明这一点，也为了让大家能看懂过程，首先引入一些简单的概念：

1.波形中心

首先我们思考一个一维的、密度不均匀的线段。我们想知道它的质心位置，也就是等效于全部质量集中一点。那么根据定义，我们取一个原点，把线段分为一个个有质量的小段dx，每个小段都有一个位置矢量。我们把各个小段dx的质量贡献矢量相加，就得到了最后的质心位置。

对于一个信号，我们同样想知道它的“质心”所在。这个“质心”就是波形中心，又叫平均时间。

如果把信号的模的平方看作时间域的“密度”，那么波形中心定义为：

s(t)是时变信号，也就是一个随时间变化的函数。

顺便给出均方平均——也就是时间先平方——的定义，下面要用。

2.时宽

知道了“质心”位置，我们自然想到，其他质量关于质心的分布如何？是均匀分布，还是不均匀分布？这个时候自然想到要算一下标准差。这个标准差就是时宽。

为防止读者一时半会儿缓不过来，展开推导一下：

按照定义，时宽描述了信号的集中程度。如果时宽小，表示信号是短持续信号；时宽大，则是长持续信号。

3.中心频率

和波形同理，中心频率就是在信号的频率域上做个积分。

4.频宽（带宽）

和时宽同理，频宽就是信号在频域的标准差。

好了我保证不会再有一个概念出现了！正式介绍信号的不确定性原理：

不确定性原理

证明：

为简化公式，不妨假设信号的时间平均、频率平均都是0，则有

由傅里叶变换的微分性质（意思就是时间信号每求一次导数，对应的傅里叶变换都要乘一个omega）

和Plancherel定理，它指出函数的傅里叶转换的平方和的积分等于函数本身平方的积分。就一维情形而言，对于ƒ ∈ L2(R)，我们有

因此，我们把

中的omega*s(omega)项用-i*ds/dt替换一下。

改写为：

又根据柯西-施瓦茨不等式，对于一个内积空间所有向量x和y，

或者写作

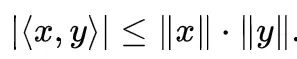
所以，对于下式：

有不等式关系：

积分一下不等式右边，利用了分部积分、和信号能量归一化的定义。

注意一下为什么

是因为我们规定了”质心“在0，这也就意味着，在正负无穷远处，应该是对称的，否则不可能质心在0，所以两个方向的极限值相减就是0。

代入就得到了

实际上海森堡的不确定性原理证明和信号的不确定性原理是类似的呦，可以思考一下。

参考资料：

维基百科

《时频分析与小波变换》 唐向宏 李齐良