【多体动力学】基础
四轮车辆模型常见的有3 7 14自由度模型,尽管建模时有俯仰、横摆自由度,但是仅在平面行驶有较高精度。没有考虑各部件都可以三维旋转、平动。在坡道转向时同时发生横摆、侧倾和俯仰,常用的简化模型先天劣势就体现出来了。
CarSim、Adams等采用多体动力学模型,精度上限高(参数不准确可能还不如简化模型准确)。如果参数合理,能更准确模拟车辆同时横摆、侧倾和俯仰的工况。

一年前做过相关工作,从简单的两个刚体常用的铰接:
到多刚体多种铰接,可以实现多种机械的仿真:
【多体动力学】履带车多体动力学模型 斜坡转向 圆柱铰 旋转铰

今天有兴趣重温了一下,整理基础内容,后续会整理进一步内容,以及讲解、实操内容。下面开始↓

刚体空间三维旋转是十分复杂的,最简单的就是欧拉角表示,即分别绕三个新生成的轴线旋转一定角度,这三个角度即欧拉角。但是存在一点瑕疵,就是第二次旋转不能出现整数倍的π/2,会出现奇点。但欧拉角仍然是伟大的,在常见系统建模上也是足够用的,也是最简洁最高效的。
本次Z-X-Y顺规内旋欧拉角为例演示,即分别绕新生成的Z、X、Y轴旋转三个欧拉角,旋转矩阵一直左乘表示矢量分量的列向量,如下图。
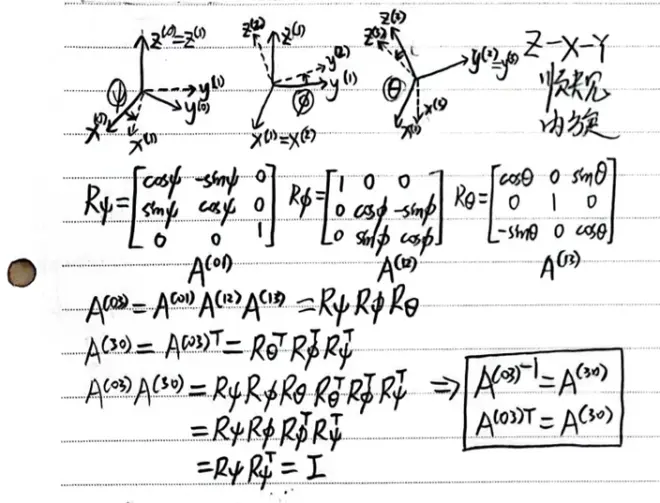
既然欧拉角是各个阶段的角度,其角速度并不是刚体系三轴的角速度。为后续计算需要推导他们的关系,矢量写成基底乘分量的形式,按照前面的旋转顺序推导如下。
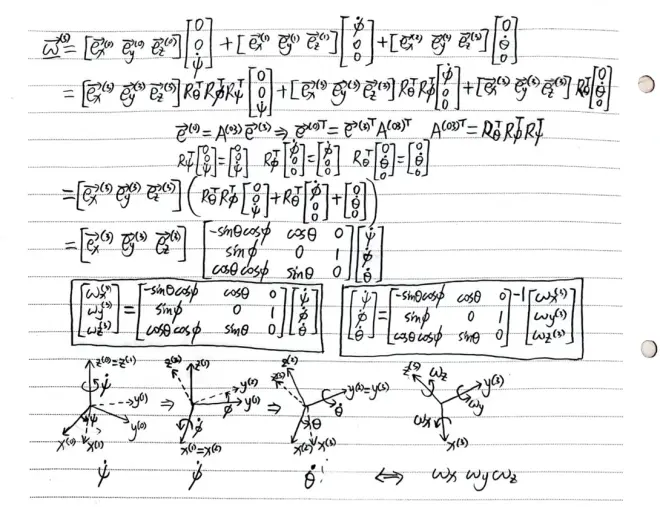
空间旋转搞定后,进行动力学部分的推导。这里以动量定理和动量矩定理为基础。推导如下


其中有些不太常见的推导过程如下,旋转矩阵求导,以及叉乘转化为反对称矩阵乘列向量。
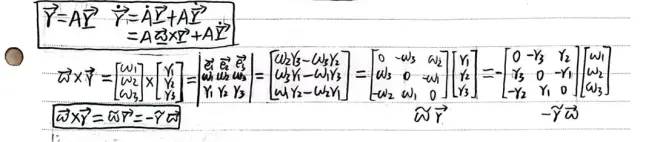
最终,就可以将所有刚体的六自由度微分方程列出,同时列出各刚体间各类铰接约束,求解方程获得各自由度的变化率和各铰接内力。

其中约束为动力学约束,可以从位置约束出发,连续求导获得动力学约束,比如下面

最终的动力学约束包含平动引起的牵连加速度、相对加速度,以及转动引起的切向加速度、法向加速度和科氏加速度。这里完全是推导获得,这样可以保证准确,而不是直接开始写动力学关系,很容易漏掉。比如像科氏加速度是推导获得的,不用刻意记忆。此外这里也解释了前面提到的旋转矩阵求导问题。

敬请期待↓

