丘成桐“证明”卡拉比猜想的逻辑错误在哪里
一,缘起
1954年的国际数学家大会上,31岁的意大利裔数学家卡拉比,在会议的邀请报告中用一页纸写下了他著名的猜想:令M为紧致的卡勒(Kahler)流形,那么对其第一陈类中的任何一个(1,1)形式R,都存在唯一的一个卡勒度量,其Ricci形式恰好是R。
卡拉比还粗略地描述了一个他的猜想的证明方案,并证明了,如果解存在,那必是唯一的。
卡拉比认为,要证明这个猜想需要两步:
第一步,证明猜想中所说的具有指定里奇形式凯勒度量的唯一性。
第二步,证明凯勒度量的存在性。
卡拉比宣称:唯一性卡拉比自己证明了。
但是卡拉比说:“对于存在性,依赖于一个积分微分方程的存在性假定”。
卡拉比提到的“典范类的凯勒流形”中与猜想密切相关的积分可微方程,进一步明确成一个蒙日-安培方程。
--------------------------------------------------------------------------------
丘成桐解释说:
1,卡拉比猜想实际上与蒙日-安培方程等价。
2,要求解的这个蒙日-安培方程,是一个很难的非线性偏微分方程。他花了将近3年时间,做了大量准备工作,发展了强有力的偏微分方程技巧,使用先验估计方法,在1976年6月求解了这个非线性复蒙日-安培方程(至多有一个解)。
3,从而给出了卡拉比猜想的证明(实际上是:丘成桐证明了其流形上复数的蒙日—安培方程,至多只有一个解。详见知乎:长篇科普:卡拉比—丘成桐定理,及其物理意义(上)
金白石https://zhuanlan.zhihu.com/p/380529964?utm_medium=social&utm_oi=26738222432256)。)。
-----------------------------------------------------------------------------
二,我们总结丘成桐证明的这个过程
1,卡拉比提出这个猜想的第二步需要证明存在性。
2,这个存在性依赖于一个积分微分方程的存在性假定。
3,这个存在性假定的东西就是卡拉比在【典范类的凯勒流形】中明确的“蒙日-安培方程”。
4,丘成桐指出卡拉比猜想与蒙日-安培方程等价。
5,丘成桐用了3年时间解开了这个“非线性复蒙日-安培方程”至多有一个解(至多有一个解不是必然有一个解;至少有一个解才是必然有解)。
---------------------------------------------------------------------------------
三,驳斥丘成桐荒谬结论
驳斥一,丘成桐说的【至多有一个解】的含义是:
1,否定至少有两个或者两个以上的解。
2,不能保证有一个解。很可能一个解也没有。
就是说,如果没有一个解的情况下,就不能说丘成桐解开了蒙日-安培方程。
驳斥二,丘成桐说的【卡拉比猜想实际上与蒙日-安培方程等价】其实就是循环论证:
就是说,论题卡拉比猜想是支撑论据蒙日-安培方程的。同时,论据蒙日-安培方程又反过来证明卡拉比猜想。
循环论证是指:论据的真实性需要论题来证明。或者两个论据中的任何一个都需要对方证明。
驳斥三,解方程不等于数学命题证明
丘成桐说开了方程-于是证明了卡拉比猜想
解方程是在原因-结构下找出结果。
解方程相关概念
1.含有未知数的等式叫方程,也可以说是含有未知数的等式是方程。
2.使等式成立的未知数的值,称为方程的解,或方程的根。
3.解方程就是求出方程中所有未知数的值的过程。
4.方程一定是式,等式不一定是方程。不含未知数的等式不是方程。
5.验证:一般解方程之后,需要进行验证。验证就是将解得的未知数的值代入原方程,看看方程两边是否相等。如果相等,那么所求得的值就是方程的解。
6.注意事项:写“解”字,等号对齐,检验。
7.方程依靠等式各部分的关系,和加减乘除各部分的关系(加数+加数=和,和-其中一个加数=另一个加数,差+减数=被减数,被减数-减数=差,被减数-差=减数,因数×因数=积,积÷一个因数=另一个因数,被除数÷除数=商,被除数÷商=除数,商×除数=被除数)。
8,等式的性质一:等式的两边同时加上或减去同一个数,等式依然成立。等式的性质二:等式的两边同时乘或除以同一个不为0的数等式的两边依然成立。
证明告诉你结果,让你按照规则给出原因-过程的必然性,把道理讲清楚。
1,证明是对一个合理的论题-命题,利用正确的演绎推理,得出必然的结论。
2,证明有一系列原则。
包括:a,命题原则。b,证明原则。
例如,命题必须是一个全称判断,命题的主项必须是普遍概念或者单独概念(不能是集合概念),命题的谓项必须根据是肯定判断还是否定判断决定是否周延。使用的词项的概念必须具有专一性-稳定性-精确性-可以检验。
又例如,证明中的推理过程使用的词项(概念)必须具有传递性。
三段论格式必须是正确的。
结论必须符合语法规则。
(内容很多,详见百度百科【数学证明】)
丘成桐哪里有水平搞清楚这些。
丘成桐至多有一个解不是必然存在一个解。如果是至少有一个解,才能算“必然存在”。
-----------------------------------------------------------
四,数学证明的论据真实性是什么?
1,建立在共识情况下的公理。
2,货真价实的定理。
3,经过严格定义的词项(概念)之间的逻辑关系才能传递,例如:
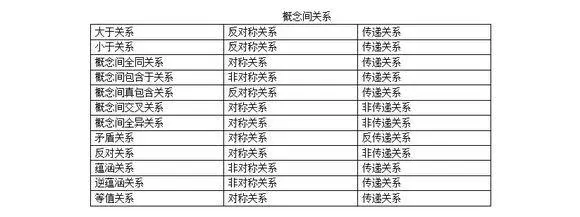
4,支撑前面论据,处于后面的论据必须是蕴含关系,不能是等值关系。(两个等值的论据不需要支撑,只要有一个就可以了),
5,命题如果是:一个方程没有解-没有整数解等(例如“费马大定理”),必须提供具体的反例。
6,一个方程有解的猜想,不是证明,而是解方程。
所以,1,丘成桐的存在性(蒙日-安培方程)是与卡拉比猜想是等值关系,充分必要条件(当且仅当蒙日-安培方程有解,卡拉比猜想成立;当且仅当卡拉比猜想成立,复蒙日-安培方程有解)。循环论证,没有任何意义。
2,解方程得出“至多一个解”不能肯定必然有解,也就是没有证明卡拉比猜想。
3,大量逻辑错误,把估计和计算当成证明。
总之,丘成桐思维混乱,就是一个数学白痴,什么也不懂。

