蒙特卡罗积分-北太天元学习27

我们可以使用蒙特卡罗模拟来近似积分的值。\int_a^b f(x) dx 可以解释成曲边梯形的面积（ 假设f(x)>=0 for all x \in [a,b] ), 蒙特卡罗方法适用于使用使用解析方法无法找到的的近似情形，尤其适用于高维积分的近似。

我们以一个简单的例子介绍一下蒙特卡罗积分方法。
我们编写蒙特卡罗模拟的北太天元脚本，以近似由y=x^2，y=0，x=0，x=1限定的曲边三角形S的面积。这实际上是 \int_0^1 x^2 dx .

当然，对于这种情况，我们可以使用解析方法找到确切的值:
        \int_0^1 x^2 dx=1/3。
使用蒙特卡罗积分，我们可以使用随机数来近似这个积分值。一种方法是从已知面积的矩形中重复选取随机点，并确定哪些点属于曲边三角形S。请注意，这个曲边三角形S完全位于单位正方形D=[0,1]×[0,1]中。我们可以通过取两个均匀的随机数x和y来选择D中的随机点。然后我们跟踪y<=x^2的次数，以及位于曲边三角形S中的随机点数。

%北太天元用Monte Carlo(蒙特卡洛)方法计算 int_0^1 x^2 dx
n = 1000;
x = rand(n,1);
y = rand(n,1);    
和 = sum(  double(x.^2 > y) );
sprintf("x^2 从0积到1的积分值是 %3.4f\n", 和/n)
ind1 = find(  y <= x.^2 );
sh1 = scatter( x(ind1), y(ind1), 'filled');
set(sh1, 'SizeData', 500);
hold on  
ind2 = find( y > x.^2 );
sh2 = scatter( x(ind2), y(ind2), 'filled');
set(sh2, 'SizeData', 500);
legend('y=x^2曲线下方的点', 'y=x^2曲线上方的点','FontSize',20)
title("蒙特卡罗方法计算 x^2 的积分")
hold off

用1000个样本点进行蒙特卡罗积分，以近似S的面积。蓝点为
曲边三角形S中的随机点，红点是不在曲边三角形S中的任意点。
红点的比例就是曲边三角形的面积:
上面北太天元代码你运行后可以能看到输出:
"x^2 从0积到1的积分值是 0.3580\n"

上面使用的是n=400, 如果把 n 增加到2000，我们可以看到

"x^2 从0积到1的积分值是 0.3330\n"

这距离精确值1/3 更加接近了。

此时蓝红点的分布如下图

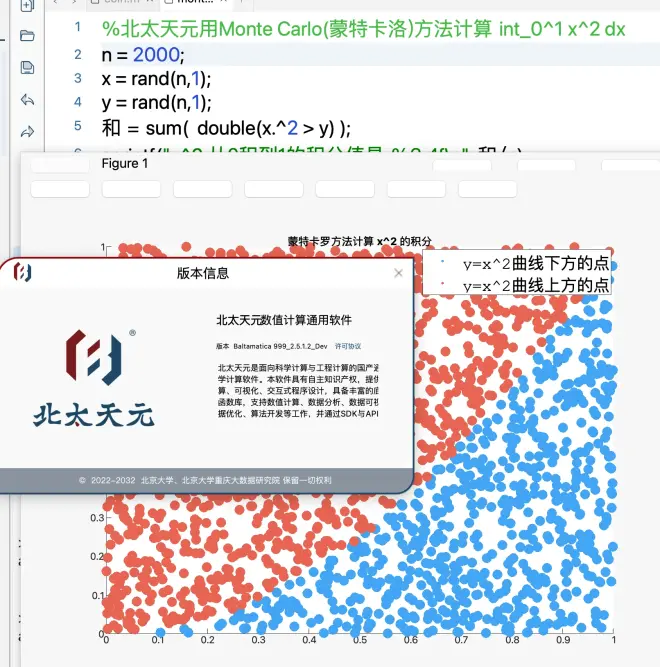
还有另一种方法来构建蒙特卡罗积分技术。假设我们想要近似曲边三角形R的面积

\int_a^b f(x) dx.

我们不是在该区域的矩形中选取成对的点而是在区间[a，b]中的随机选取x_i, 一次选取就称为一个实验。如果我们重复这个实验，f(x_i)的平均值应该接近 1/(b-a)\int_a^b f(x) dx 的平均值。在适当的条件下，可以证明当n逼近∞时，f(x_i)*(b-a)逼近积分值 \int_a^b f(x) dx.

在北太天元学习系列中的，我们介绍了可以使用北太天元的内置函数rand
得到服从[0，1]上的均匀分布的随机数，然后做一个伸缩平移变换后得到
y=（b−a）x+a 是一个服从[a,b]区间上的均匀分布的随机数。因此，上面我们介绍的
[0,1]向上的积分方法可以用这个方式迁移到[a,b]上的积分。

与任何数值积分方法一样, 我们不能期望一定完全精确地得到积分值。使用蒙特卡罗方法，我们可以观察到误差随着随机样本数量的增加而减小。在蒙特卡罗积分法中，
通过计算平均值A_n= ( f(x_1)+...+f(x_n) )/n 作为近似积分值。有定理表明
A_n的方差接近 σ^2/n。 虽然我们可能不知道σ，但我们知道增加n会导致A_n的方差
以1/n成比例的速率减小。从而，标准偏差以与1/sqrt(n) 成比例的速率递减.

北太天元可以用下面的命令来计算 \int_0^{1} x^2 dx 的数值积分
大家可以观察到误差大致还是随着n增加而减小。
for k=1:8
 n = 100*2^k;
 disp(sprintf("n = %d , 误差 %f \n",n ,  abs( mean( ( rand(n,1) ).^2  ) -1/3) ));
end

  1x1 string
    "n = 200 , 误差 0.002196 \n"
  1x1 string
    "n = 400 , 误差 0.001769 \n"
  1x1 string
    "n = 800 , 误差 0.006589 \n"
  1x1 string
    "n = 1600 , 误差 0.001157 \n"
  1x1 string
    "n = 3200 , 误差 0.001773 \n"
  1x1 string
    "n = 6400 , 误差 0.004136 \n"
  1x1 string
    "n = 12800 , 误差 0.002946 \n"
  1x1 string
    "n = 25600 , 误差 0.001589 \n"