《高等数学》同济版 全程教学视频（宋浩老师）

更新中，目前5-4到7-4,学习顺便记笔记，有帮助的话可以看一看（笔记划累了就去专栏里划吧哪里划的快一点）

5-4定积分换元法笔记

一.换元注意事项：

（1）第二类换元法时令t=某个x函数的时候，要变化上下限：即要令

x=下限，t=某个值（带入上限）

x=上限，t=某个值（带入下限）

个人总结

1.找到换元的函数,求出x=多少t，dx=多少，

2.找出上下限；令原函数等于上下限的值，并且将他们一一对应（原上限对应现上限，原下限对应现下限）

3.带入相应的原式，并求出他们（原函数！！不要忘记）在用牛顿莱布尼茨公式带入上下限求出他们的定积分

（2）例题

例1

例2

两个证明问题：

例题3-1

例题3-2

证明思想：令x=π-t的换元方式（为了凑出π/2能够使sinx，cosx变化而设）

二.相关公式：

二-1.奇偶性公式

理解图像 左偶，右奇

二-2.周期公式

（1）公式

公式1.

T为f（x）函数的周期

公式2.

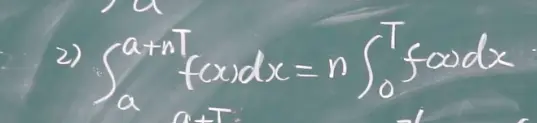
T为f（x）函数的周期

（2）例题

例题1（7）

结果位2根号2cost(自己算的)

例题2（8）

（1.）运用寄偶性，和（2.）巧妙地设分母为平方加一个常数的形势！！！！变化时候变出tanx

结果为 27/2 +3pi/2(自己算的)

例题3（9）

>>分段函数不能直接带的先换元

结果为 1/2+1/2e^4(自己算的)

5-5定积分分布积分笔记

一.公式概念：

（1）基本公式

（1-1）例题1

（1-2）注意！！！：定积分中dx的函数一定要把它给求出来。

千万不要像下面这样，不规范（写在草稿纸上）

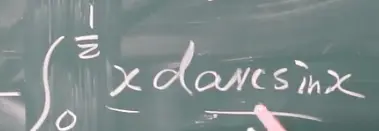
二.相关例题

第1题.（2-1）注意！！！：不能忘记：换元一定要对应上下限。

（2-2）完整过程：

第2题：

遇到右边式子出现左边要算的式子不要慌如果式负号或正号不为1拿到右边就可以了，

如果为+1那就不慌也得慌，慌完检查重新算.

5-6无穷限的反常积分

+

5-7无界函数的反常积分

相关例题

一.定义与类型

1-1（反常积分的定义）

（1）上限或（2）下限或（3）上下限都为无穷的积分就叫反常积分；

1-2（反常积分的类别）

（1）正无穷的反常积分：有极限收敛，没极限发散，t趋向正无穷

（2）负无穷的反常积分，有极限收敛，没极限发散，t趋向负无穷

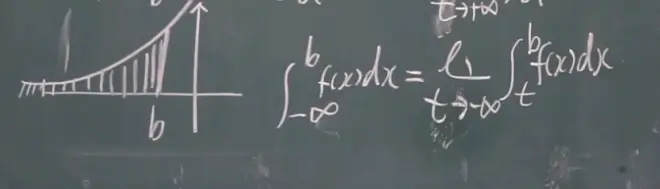
（3）负无穷到正无穷的反常积分，注意，相加得到这个极限（负无穷到正无穷）的极限如果有一个是发散的不收敛那么这个极限（负无穷到正无穷也不收敛）就不收敛。

二.反常积分的牛顿莱布尼茨公式的运用

1-1广义莱布尼茨公式

其中假设f（x）的原函数为F（x）。直接带上下限。【广义莱布尼茨公式】

1-2例题

第（1）题

第（2）题

步骤1

步骤2

第（3）题

1。思路讨论

假设等于2（p>1），极限为0已经收敛了，更小一定收敛

假设等于1/2（p<1），等于1/2时x上下同时乘以根号可以知道结果应为无穷大所以取倒数（p<0）的话则会更快趋于无穷大。所以发散。

2.证明

p=1

p ！=1（不等于）

5-8伽马函数

定义：

两个性质结论：

（1）

（2）

结论（1）推导

结论（2）推导

定积分的应用

6-1定积分的应用微元法(元素法)

一：微元法的公式：

（1）正常微元法

就是将某个部分的面积为【图形中为小正方形dx*f（x）】求法应用到区间[a，b]就是定积分的几何意义.

（2）极坐标微元法公式:

近似看成扇形：

关于将某个不规则函数用微元法思想推导成一个扇形得到的公式::

6-2定积分的运用

一、微元法的面积公式：

A为面积近似值.

二、两种微元法求面积方法与例题

例题1.求阴影部分面积

1.x型区域的做题方法：

（ 帮助理解）

（最终结果）

【函数上减下的微分】

结果：1/3（个人计算）

2.Y型区域的做题方法

【函数右减左的微分】

易错点！：求导是对y求导dy。而不是dx，要化成x对y的函数x=什么y的形式

X是函数，Y是自变量

3.关于X型区域和Y型区域如何选择:

（1）.函数的边缘垂直与X轴选用X型区域的方法

（2.）函数的边缘垂直与y轴选用Y型区域的方法

（3.）难说型（3）”逝一逝“尽量找到只用分成一部分定积分的来做,而不是用两部分的

三、例题：

例题2：求阴影部分面积

宋式秒杀法：用笔垂直x轴或y轴移动，分别找到右边-左边（Y型区域）和上边减下边（X型区域）来构造公式

例题3：求阴影部分面积:

【1】用X型区域求面积的方法

【2】（简便方法）由于左右对称的可以只用求一边*2既可以得到结果

6-3定积分的应用--求面积（二）接上一节 

例题3：求下列阴影部分的定积分

图形部分:

使用y型区域的方法

6-4定积分的应用--求面积极坐标情形

例题4

1.求扇形面积的定积分坐标公式

(也是求极坐标方程的面积公式):

例题5：：

结果

6-5定积分应用旋转体的体积

一.定义与公式

a-b上截面面积的定积分

放大后：

就是用微元法分成无数个部分的面积.

二.相关例题；

1.1绕x轴旋转的

把y当作自变量x，x当作因变量y，再用公式计算

例6.

例7.

（绕y轴的方向旋转）

.（绕x轴的方法求解）

例8.

另一个例8.

一个半圆中间截取一部分的旋转

t的范围不同

由于是y周旋转，所以是从x=2pi的位置的y旋转到x=pi位置的所以2pi写在下面(2pi时候的面积大于pi)所以

要注意区间上下限写的位置应该反过来

例9.

例10.(正劈锥体)

1.2绕y轴旋转的：

主要公式：

把x看作半径，用f（x）dy的微积分去计算，

6-6求平面曲线弧的长度 

一.定义公式：

公式一：

用线段近似弧的长度，假设弧是【参数方程】

解决看成参数方程的曲线弧。

公式二：

公式三：

给极坐标求曲线弧

推论（可看可不看）：

相关例题：

例11.

结果：2\3(a+1)^3\2 - 2\3(b+1)^3\2

例12：

结果8a

例13：

运用和极坐标有关的弧长方程解决问题。

（自己算结果），更号下(1+4pi^2) -(2pi) +(arctan2pi)

微分方程

7.1微分方程的基本概念：

一.定义：

1.1微分方程：含导数(不一定是一阶导数)的方程就叫微分方程

1.2微分方程的阶数:求一次导就是一阶

二.通解与初值条件

通解：方程含常数的个数与微分方程相同就叫微分方程的通解

初值（始）条件：

如经过（1，2）这个点就是这个题目的初值条件

初值条件：用于确定方程的解中任意常数的附加条件，称为微分方程的初始条件

7.2可分离变量的微分方程

一.定义（什么是可分离变量方程）

1.1可分离变量方程的形 式：

即为：

将带x的式子放到一边，把含y的式子放到一边，在去求微分。就是可分离变量方程

二.相关例题：

例题0：（最左边为题目）

例题1:

例题3（物理题）:

7.3齐次方程：

（补充）定义：即未知数次数都相等的，右端等于0，左端是含未知数的项，这样的方程就是齐次方程

一.齐次方程的基本概念

形如图中的方程形式就是齐次方程

（1）方程是y/x看成整体的一个函数，都是对x求导

（2）根据图中的1.2.3三个步骤求出三个量，最后转换成为u和x的方程再进行可分离变量求解就行

二.可化为齐次方程的形式

（1）宋氏对称

xy的次数相对的情况，这时候可以用除x的n次方的形式来变换形式（判断是否使用齐次方程小技巧）

三.例题：

例题1

情况一：

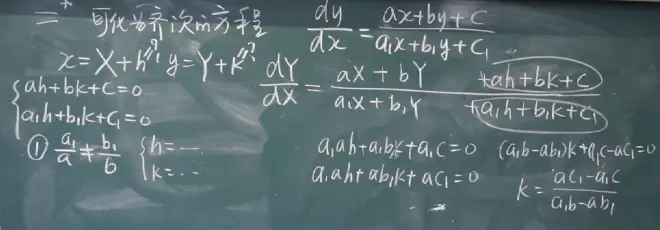
a1\a不等于b1\b

情况二：

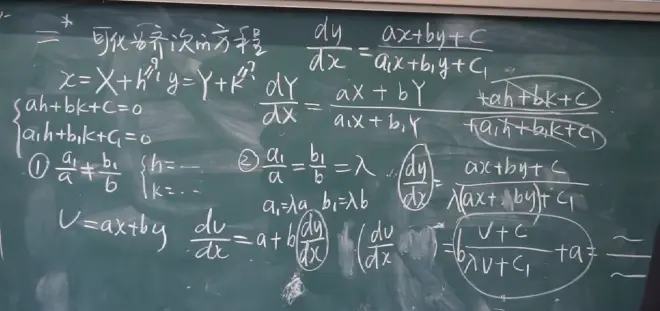
a1\a=b1\b

7.4一阶线性方程 ：

1.方程相关定义：

形如下面的方程就是一阶线性方程

推论公式（主要记住）

推论过程

2.伯努利方程（不努力方程）：

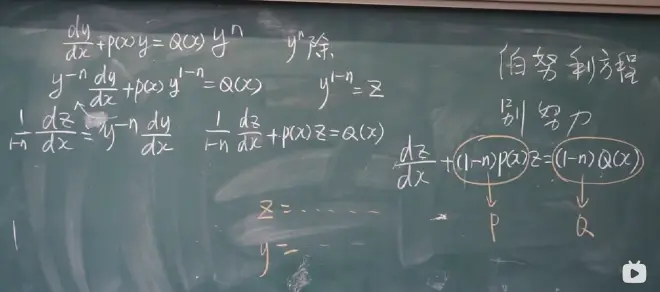
3.相关例题

例1：

例3

结果x=u-ln（1+u）

y=ln(1+u)

例4：（伯努利方程）