椭圆中的“圆幂定理”

如图:过点(不在椭圆
上)的直线
、
分别与椭圆
:
(
)交于
、
和
、
,则:
注1:其中、
分别为直线
、
的方向半径.
注2:直线的方向半径指的是与直线平行或共线的半径.


证明:设点的坐标为
,
直线、
的倾斜角分别为
、
,
直线、
的方向半径分别为
、
,如图:
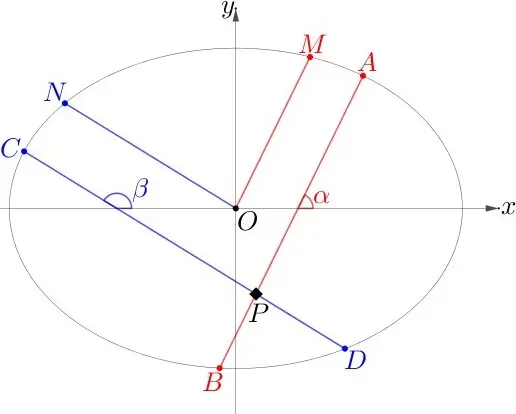
设直线的参数方程为
(为参数),
与椭圆联立解得
,所以
,


设直线的参数方程为
(为参数),
与椭圆联立得
,
所以


所以,


同理可得


所以.
证毕.

