向量究竟是什么？

向量的线性组合，基与线性相关

矩阵与线性相关

矩阵乘法与线性变换复合

三维空间中的线性变换

行列式

逆矩阵，列空间，秩与零空间

克莱姆法则

非方阵

点积与对偶性

叉积

以线性变换眼光看叉积

基变换

特征向量与特征值

抽象向量空间

快速计算二阶矩阵特征值

张量，协变与逆变和秩

目录

叉积

以线性变换眼光看叉积

叉积

前面章节介绍了向量的点积，并从线性变换角度展示了其几何意义，今天我们再来看向量的另一种重要操作：叉积，同样的，除了叉积的标准计算公式外，我还会从线性变换的角度来做深入理解。

如上图所示，让我们把证明的部分放到后面，先给出叉积的定义：向量和向量叉积的结果就等于其张成平行四边形的面积，且如果在右侧，结果是正的，在的左侧，结果就是负的，对于叉积来讲，这意味着顺序很重要。

这里再一次出现了四边形面积的概念，这就让我们想起了前面讲的矩阵行列式的几何意义，如果在求向量叉积时不知道该平行四边形的面积，这时就可以换个思路，通过求行列式的值来计算叉积的结果。

对于，将作为矩阵的第一列，将作为矩阵的第二列，然后计算矩阵的行列式作为叉积的结果，那为什么和组成的矩阵的行列式就是叉积的结果呢？

如下图所示，由和组成的矩阵与将和分别移至和的线性变换是相对应的：

如下图所示，行列式就是变换前后面积变化比例的度量，变换前由和组成的正方形的面积为1，经过变换后这个正方形就变成了我们想要的平行四边形，而用来度量面积变化比例的行列式直接给出了平行四边形的面积，因为他是从面积为1的正方形变换得来的。

如下图所示，行列式的计算规则也正好满足叉积定向计算法则，也就是当v在w左侧时，叉积结果为负，行列式结果也为负数。

同理，也可以得到叉积的如下性质：当两个向量越接近垂直时面积越大，也就是叉积越大，越接近平行时，叉积越小。

注意，前面讲的内容看似很有道理，但是，它并不是叉积真正的含义，叉积的结果并不是一个标量值，而是一个向量，如下图所示，真正的叉积是通过两个不同的三维向量生成一个新的三维向量。

但叉积和前面讲的平行四边形面积仍然有很大关系，如下图所示，叉积的结果是一个向量，向量的长度等于平行四边形的面积，向量的方向垂直于平行四边形。

当然，垂直于四边形的向量有两个，一正一反，哪个才是叉积的结果向量呢？如下图所示，这时就要用到右手定则，右手食指指向v的方向，中指指向w的方向，此时，拇指指向的方向就是叉积结果向量的方向。

那么，叉积的计算方式可以定义成下面的方式：

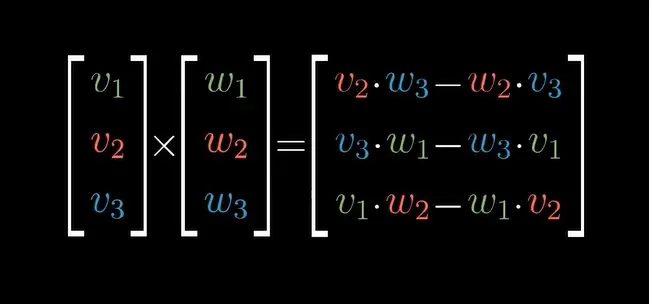
即便如此，我们仍然可以将向量的叉积转换成行列式的计算上，如下图所示，矩阵的第一列是基向量，第二列，第三列为v和w的坐标，行列式的结果就是叉积结果。

然而，这种方式容易让人产生困惑，让向量作为矩阵的元素是什么意思？要理解这个需要用到前面用到对偶性的知识，我们下一章节会具体讲解。

以线性变换眼光看叉积

    本章节的主要内容就是从线性变换的角度来证明一下上面这个公式，也就是让大家理解叉积的几何意义，要想理解本章节的内容，需要大家掌握前面学习的知识：行列式和对偶性。

这里给大家做个简单的回顾：

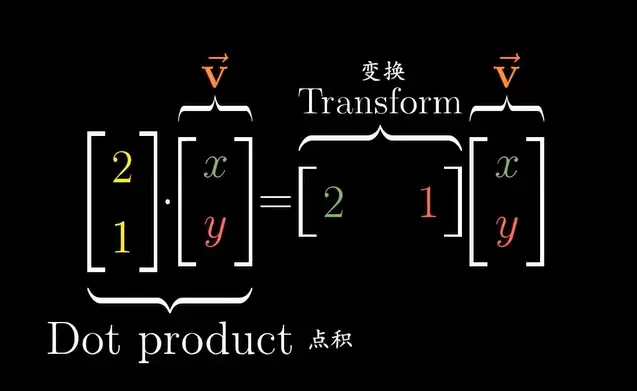
    对偶性是指每当看到一个从多维空间到一维数轴的线性变换时，该线性变换都有一个与之相对应的向量存在， 如下图所示，二维空间基向量经过线性变换后分别落在了4和1的位置，根据前面学的知识可知该线性变换就是[4,1]，如果将1*2的矩阵竖着写就变成了与之对应的对偶向量，这是不是有点像转置操作？

如下图所示，当对多维空间中的向量应用该线性变换时，等价于该多维空间向量与该对偶向量做点乘。

有了前面的知识铺垫，接下来让我们正式开始叉积的理解：

    二维空间的对偶性同样适用于多维空间，首先根据向量和定义一个从三维空间到一维数轴的某种线性变换，然后我们找到与这个线性变换相对应的三维对偶向量，假设叉积就是该对偶向量，对偶向量也就是该线性变换。

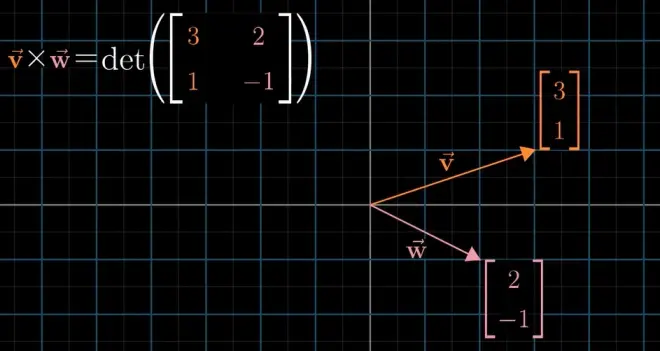
现在让我们再来回顾一下二维版本的叉积的定义，如上图所示，将向量作为矩阵的列，然后叉积的结果就是由向量组成平行四边形的面积，也就是该矩阵的行列式。

现在我们把二维版本的叉积定义推广到三维中，如上图所示，三个向量的叉积就是三个向量组成平行六面体的体积，也就是矩阵的行列式。

当然上面的叉积定义并不是真正的叉积定义，真正的叉积结果是一个向量，但这却给我们提供了一种思路，如上图所示，我们把上面的u替换成未知量，v和w不变，这样我们就得到一个从三维空间到一维数轴的函数了，该函数的几何意义是：对于任意一个输入向量（x,y,z），都会有该向量和v， w构成的平面一起确定一个平行六面体，平行六面体的体积等于一个数，该函数就是输出这个体积。

虽然这个函数有点无厘头，但我们暂时按照这个思路去理解它，这对理解叉积很关键，因为该变换是线性的。且是从三维到一维的变换，所以我们就能用到前面的对偶性思想了。

既然是从三维空间到一维空间的变换，如上图所示，就存在一个1*3的矩阵来表达上面的线性变换，根据对偶性的思想，可以转换为向量的点积，我们用向量代表该变换.

我们先把等式两边计算展开，显然，v和w的特定组合就是我们要寻找的p的坐标分量。

如上图所示，让我们再回顾一下前面叉积的计算方法，这两个公式是不是有点关联？让我们继续沿着这个线索探索下去。

如上图所示，什么样的向量P能满足下面这些特质呢？P与未知向量（x,y,z）的点积的结果等于该未知向量与v，w组成的平行六面体体积，等式左边，如下图所示，我们知道点积的几何意义是未知向量到P的投影长度与向量P长度的乘积。

等式右边，如下图所示，平行六面体的体积等于底乘以高，底就是v和w组成的平行四边形的面积，高是（x,y,z）到平行四边形垂直方向上的投影，

 P满足什么条件能让等式相等呢？只有P是v和w的叉积向量时，等式才会相等，等式左边：P的长度*（x,y,z）到P的投影长度，等式右边：平行四边形的面积*（x,y,z）到四边形垂直方向的投影，如果P时v和w的叉积结果，那P的长度就等于平行四边形的面积，且P是垂直于v和w形成的平行四边形。