OpenGL实例教程10:透视投影
为什么需要透视投影?
模型都是3D的,但屏幕是2D的。如何将3D空间投影到2D平面,还能保持深度的视觉效果?在OpenGL中,采用透视投影矩阵作用顶点来实现,即完成缩放、选择、位移之后,进行透视投影的操作。就像下面的铁轨,越远的地方,在2D屏幕上占比越小。

透视投影参数介绍
生成透视投影变换需要4个参数:
宽高比:矩形区域的宽度和高度之间的比率
垂直视场角:相机的垂直角度,通过它来观察世界
近/远Z平面:裁剪离相机太近/远的物体

宽高比:
标准化空间的X,Y坐标都是-1到1之间(这里的数值是抽象的概念,将代表精度的分配)
电脑屏幕往往都宽度大于高度
标准化后,X,Y坐标都是-1到1,但刻度含义不同
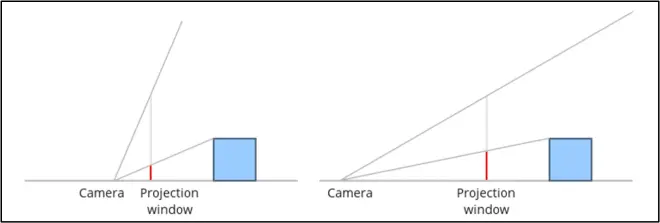
垂直视场角:
屏幕大小是固定不变的
左图:值大,显示范围大,分配给物体的屏幕区域就小(模拟缩小)
右图:值小,显示范围小,分配给物体的屏幕区域就大(模拟放大)
近/远Z平面:
标准空间Z坐标是-1到1之间,需要映射到近平面到远平面之间的距离
透视矩阵
需要一个矩阵,能完成透视投影的变化:

矩阵的推导过程如下:
1、宽高比( ar:aspect ratio)计算如下:
宽高比(ar) =屏幕宽/ 屏幕高
为方便计算,高度设为2,这意味着宽度正好是ar的两倍。如果把相机放在原点,从相机背后看这个区域,会看到:

2、现在让从“侧面”看看,通过垂直视场角计算相机到投影平面的距离(由角度alpha表示):

3、计算Y的投影坐标:

4、同样的方法可以计算X的投影坐标:

5、将X,Y的投影坐标映射到标准化坐标[-1,1]:

6、现在需要一个矩阵,第一行为(a,b,c,d),能满足下面的运算:

可以选择‘b’和‘d’为0,但无法找到合适的‘a’和‘c’。OpenGL采用的解决方案是将转换分为两步:
1、与投影矩阵相乘;

2、与Z值做除法(GPU自动完成)。
每个顶点Z的值都可能不同,所以不能把它放到变换矩阵中(uniform变量),在步骤6中,将自动除以Z,那么所有的顶点Z值都将变为1,即都丢失了原始值。为了解决这个问题,将用W保存Z值。
7、将Z的投影坐标映射到标准化坐标[-1,1],并且需要考虑近/远平面的影响:
需要选择矩阵第三行的值,以便在系统自动除以w后,任何在可视范围内的Z值(即NearZ <= Z <= FarZ)将被映射到[-1,1]范围。
由一般函数表示(变换矩阵第三行将起到等效的作用):𝑓(𝑧)=𝐴∙𝑧+𝐵
经过透视除法后:𝐴+𝐵/𝑧
当Z等于近平面时,结果一定是-1,当Z等于远平面时,结果一定是1。因此:

8、现在需要选择矩阵的第三行作为向量(a b c d),它需要满足:

可以将` a `和` b `设置为零。然后A值可以变成` c `, B值可以变成` d `(因为已知W是1)。
因此,最终的变换矩阵为:

透视投影代码实现
直接调用库即可,无需自己实现,库的主要代码如下:
Opengl应用程序代码
运行效果


