[光线追踪] 02 -- 渲染模型

2022-05-21 14:29 作者:nyasyamorina 0人读过 | 我要投稿

在上一篇专栏里面. 认识了几个辐射学名词, 定义了光线, 以及了解了描述光在不透明物体表面传播的BRDF. 这篇专栏就简述几种不同的渲染模型. 并且在专栏最后, 略微讨论一下光追的收敛性.

光线类

在上一篇专栏里定义了光线为穿过无限小平面的平行光. 这里需要对光线进行代码实现 (其实是上一篇忘记了). 光线需要定义光的起点以及方向, 尽管方向是立体角变量, 但为了方便计算, 方向还是使用一个 Vec3 类型表示, 而不是两个浮点数 θ, φ. 在给出了起点 p 和方向 d 后, 光线上任意一点都可以由 p + t * d 给出, 其中 t 是大于等于 0 的浮点数.

另外不得不说的是, 在一部分渲染模型里, 运行 d 的模长不等于 1, 这是因为模长可以被上式的 t 修正. 但在我这里选用的模型里, 因为经常需要计算 d 与其他向量的点乘, 如果模长不为 1 就会导致计算错误. 尽管这里要求 d 的模长为 1, 在构建光线类型时不会强制对输入进行归一化, 方向的归一化应该根据构建光线前的实际情况可选地进行 (因为归一化非常吃性能).

如此, 光线类为:

另外, 光线不需要给出辐射度/颜色的原因是, 在反向光追(见下)里, 每条光线的颜色都依赖于下一条光线的颜色, 在求得某条光线的颜色时, 这条光线已经没有用了.

光线的传播 -- 正向与反向

在现实里, 光是从光源出发直接或间接地射入传感器, 从而产生所见的图像. 那么模拟光线从光源开始, 在传感器结束的渲染就叫做正向光线追踪. 正向光线追踪的缺点就是, 从光源开始的光线可能只有一小部分在传感器处结束, 而大部分会发散到开阔的空间里或终止于较深的光线迭代过程里, 从而造成较大的性能浪费.

所以提出了反向光线追踪: 光线从传感器开始, 在光源结束. 从传感器开始确保了每条光线都对渲染都是有贡献的, 从而使性能不在这方面造成浪费. 但反向光追的缺点也是显而易见的: 为了得到正确的渲染图像, 必须假设场景内发生改变光线的事件都是可逆的, 亦即几何光学里的光路可逆, 所以反向光追仅能渲染满足几何光学的图像, 而不能渲染满足波动光学的图像 (准确来说是不能渲染有关磁效应的波动光学图像). 接下来所有讨论都是基于反向光追来讨论.

渲染模型

确定需要使用的渲染模型就等于确定了渲染代码的逻辑. 光追里由常用两种渲染模型: 半球模型和面积模型. 这里仅介绍一下两种模型, 至于何时选取合适的模型则留到下一篇专栏里讲述.

在介绍模型前, 首先确定数学符号. 如同上面光线类里面所说, 方向可以使用立体角 (θ, φ) 或向量 (x, y, z) 表示. 为了方便, 方向统一使用全局坐标系的向量 $%5Cvec%20%5Comega$ 表示, 但出现立体角符号 (主要是θ) 时, 表示的是在局部坐标系下的方向. 如下图所示

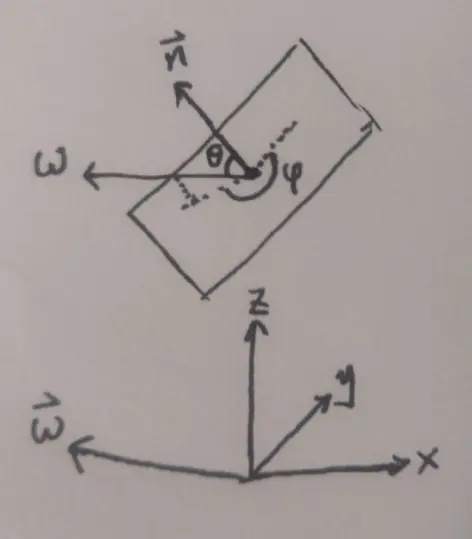
为了确定场景里事件的位置, 可以给几乎全部的变量加上位置 p, 并且 p 必定在物体表面上, 那么点 p 处的 BRDF 可以写为 $f_r(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_i%2C%5Cvec%7B%5Comega%7D_o)$ , 其中 ωᵢ, ωₒ 是入射和出射光方向, 并且两个方向都是远离 p 点的. 相应的入射/出射光可以表示为 $L_i(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_i)$ 和 $L_o(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_o)$ .

半球模型

半球模型是简单建立在求解出射辐射度的式子上的. 给式子加上物体表面的自发光辐射度 Lₑ, 那么出射辐射度为 $L_o(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_o)%3DL_e(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_o)%2B%5Cint_%7B2%5Cpi%5E%2B%7Df_r(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_i%2C%5Cvec%7B%5Comega%7D_o)L_i(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_i)%5Ccos%5Ctheta_i%20d%5Cvec%7B%5Comega%7D_i$ .

不难知道, 点 p 处的入射光必定是场景里另一个点的出射光 (天空可以看作无限远处的半球物体). 那么假设有一个函数 h 返回场景里与光线碰撞的最近点, 如下图所示

那么有 $L_i(%5Cvec%20p%2C%20%5Cvec%7B%5Comega%7D_i)%3DL_o%5Cleft(%5Cvec%20h(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_i)%2C-%5Cvec%7B%5Comega%7D_i%5Cright)$ , 为了保证这条式子成立, 必须假设光线传播时不会衰减或发生散射. 那么点 p 处的出射辐照度为 $L_o%5Cleft(%5Cvec%20p%2C%20%5Cvec%7B%5Comega%7D_o%5Cright)%3DL_e%5Cleft(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_o%5Cright)%2B%5Cint_%7B2%5Cpi%5E%2B%7Df_r%5Cleft(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_i%2C%5Cvec%7B%5Comega%7D_o%5Cright)L_o%5Cleft(%5Cvec%20h%5Cleft(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_i%5Cright)%2C-%5Cvec%7B%5Comega%7D_i%5Cright)%5Ccos%5Ctheta_id%5Cvec%7B%5Comega%7D_i$ .

这条式子即是半球渲染模型, 在模型里仅有 Lₒ 未知, 并且 Lₒ 同时也是求解项.

面积模型

对半球模型进行修改可以得到面积模型. 在半球模型里, 积分范围是在点 p 处的上半球, 而在面积模型里, 积分范围则是场景内的全部物体表面.

由于从任意表面发出的光线, 可能在到达 p 点前被阻挡. 定义函数 $v(%5Cvec%20p%2C%5Cvec%20q)$ , 如果 p, q 两点之间没有任何物体阻挡, v 返回 1, 否则返回 0. 实际上, v 可以由 h 定义出来: $v(%5Cvec%20p%2C%5Cvec%20q)%3D%5Cleft%7C%5Cvec%20h(%5Cvec%20p%2C%5Cfrac%7B%5Cvec%20q-%5Cvec%20p%7D%7B%7C%5Cvec%20q-%5Cvec%20p%7C%7D)-%5Cvec%20p%5Cright%7C%5Cmathrm%7B%5C%20is%5C%20equal%5C%20to%5C%20%7D%7C%5Cvec%20q-%5Cvec%20p%7C$ , 这里假定 true = 1, false = 0. 并且有立体角与单位面积的关系 $d%5Comega%3Dd%5E%7B-2%7D%5Ccos%5Ctheta%20dA$ , 那么可以把半球模型改写为面积模型:

$L_o%5Cleft(%5Cvec%20p%2C%20%5Cvec%7B%5Comega%7D_o%5Cright)%3DL_e%5Cleft(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_o%5Cright)%2B%5Cint_Af_r%5Cleft(%5Cvec%20p%2C%5Cvec%7B%5Comega%7D_i%2C%5Cvec%7B%5Comega%7D_o%5Cright)L_o%5Cleft(%5Cvec%20q%2C-%5Cvec%7B%5Comega%7D_i%5Cright)v%5Cleft(%5Cvec%20p%2C%20%5Cvec%20q%5Cright)%5Cfrac%7B%5Ccos%5Ctheta_%7Bi%2C%5Cvec%20p%7D%5Ccos%5Ctheta_%7Bo%2C%5Cvec%20q%7D%7D%7B%7C%5Cvec%20q-%5Cvec%20p%7C%5E2%7DdA(%5Cvec%20q)$ , 其中 $%5Cvec%7B%5Comega%7D_i%3D%5Cfrac%7B%5Cvec%20q-%5Cvec%20p%7D%7B%7C%5Cvec%20q-%5Cvec%20p%7C%7D$ , 如下图所示

光追的收敛性

从上面模型看出, 最终的渲染图像是无法通过直接解方程求出的. 但因为求解项 Lₒ 也依赖于 Lₒ 自身, 所以可以通过迭代步骤求出 Lₒ 的近似解. 这里需要讨论一下求解 Lₒ 的收敛性.

上面两种模型都可以概述为 $L_o%3DL_e%2BK%5Ccirc%20L_o$ , 其中 K 就是代表积分部分. 因为积分是线性算符, 所以有 $K%5Ccirc%20L_o%3DK%5Ccirc(L_e%2BK%5Ccirc%20L_o)%3DK%5Ccirc%20L_e%2BK%5E2%5Ccirc%20L_o$ . 所以最终 Lₒ 可以由 $L_o%3DL_e%2BK%5Ccirc%20L_e%2BK%5E2%5Ccirc%20L_e%2B%5Ccdots%3D%5Csum_%7Bn%3D0%7D%5E%7B%2B%5Cinfty%7DK%5En%5Ccirc%20L_e$ 给出. 由泰勒级数知道, 这条式子形式上等价于 $L_o%3D(1-K)%5E%7B-1%7D%5Ccirc%20L_e$ , 并且级数收敛的条件为 $%7CK%7C%3C1$ .

上一篇专栏里给出了反射率 ρ, 并且 ρ 与出射/入射方向无关. 把 ρ 放进函数试验空间里, 并假定 $L_i(%5Comega)%3D%5Cdelta(%5Comega-%5Comega_i)%3D%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%2B%5Cinfty%2C%5C%2C%5Comega%3D%5Comega_i%5C%5C0%2C%5C%2C%5Comega%5Cneq%5Comega_i%5Cend%7Bmatrix%7D%5Cright.$ , 那么在指定了入射方向 ωᵢ 后, 反射率为 $%5Crho_%7B%5Comega_i%7D%3D%5Cint_%7B2%5Cpi%5E%2B%7Df_r%5Cleft(%5Comega_i%2C%5Comega_o%5Cright)%5Ccos%5Ctheta_od%5Comega_o$ , 这条式子代表了光线照射物体表面时, 从表面射出的总能量与光线能量的比值, 并且实际物体必定有 $%5Crho_%7B%5Comega_i%7D%3C1$ . 由光路可逆条件, 以下式子也是成立的 $%5Crho_%7B%5Comega_o%7D%3D%5Cint_%7B2%5Cpi%5E%2B%7Df_r(%5Comega_i%2C%5Comega_o)%5Ccos%5Ctheta_id%5Comega_i%3C1$ .

回到算符 K, K 在半球模型里表述为 $%5Cint_%7B2%5Cpi%5E%2B%7Df_r(%5Comega_i%2C%5Comega_o)L_o%5Ccos%5Ctheta_id%5Comega_i$ . 可以观察到, K 在函数试验空间里与上面的 $%5Crho_%7B%5Comega_o%7D$ 等价, 亦即 |K| < 1 的充分条件为 $%5Crho_%7B%5Comega_o%7D%3C1$ . 并且由于面积模型是半球模型的重新表达, 所以面积模型也符合这个条件. 由此得到了光追收敛性的充分条件: 光线传输必须符合能量守恒 (算上被物体吸收能量).