实分析——第六章——抽象测度和积分理论(4)
接下来我们考察极坐标的积分公式:

首先对一些符号做出一些决断:


首先认定:

为了证明**这个结论,接着我们首先取E1,E2:

此时我们再取:

再有:

回到证明(9),先由于先前的证明,我们很容易得到:

那么:

最后我们来看lebesgue——stieltjes积分


证明如下
第一步:

第二步:
目标:
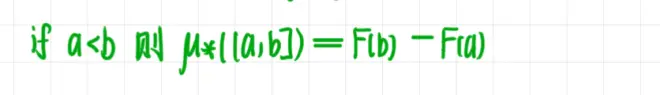
一边:
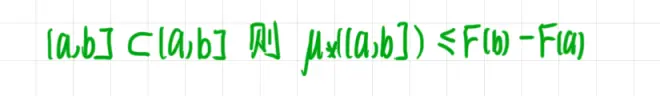
另一边:

目标得证。
第三步:证明它是度量外测度。

第四步:则在Bore集上:

第五步,证明唯一性:


第六步,证明反过来的情形:

接下来我们考察极坐标的积分公式:

首先对一些符号做出一些决断:


首先认定:

为了证明**这个结论,接着我们首先取E1,E2:

此时我们再取:

再有:

回到证明(9),先由于先前的证明,我们很容易得到:

那么:

最后我们来看lebesgue——stieltjes积分


证明如下
第一步:

第二步:
目标:
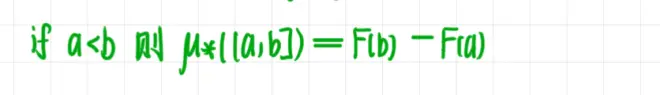
一边:
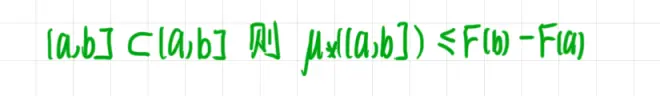
另一边:

目标得证。
第三步:证明它是度量外测度。

第四步:则在Bore集上:

第五步,证明唯一性:


第六步,证明反过来的情形:
