[Quant 1.7] 从数理的角度理解一下RNN (2)

我先放资源

第一个是MIT的一本深度学习教材的RNN章节，作者是Ian Goodfellow & Yoshua Bengio & Aaron Courville

https://www.deeplearningbook.org/contents/rnn.html#pf7

第二个是吴恩达 (Andrew Ng)博士的网课

吴博士的网课主要从NLP的角度出发介绍RNN，里面有帮助的理解的例子。但是它的notation我看不太习惯。然后那本教材我感觉是给更厉害的quant或者数据科学/AI专业的学生读的，细节非常之多，我个人啃起来感觉吃力。这篇想把零零散散的知识点总结一下。（以下内容可能有很多理解错误的地方，后续我发现问题的话会编辑。然后我会有很多中英文穿插着，毕竟面试可能会被问到，我也借这个专栏强化一下记忆。）

4. RNN和它的两个弱点：梯度消失和梯度爆炸

这一步基本上我见过的所有视频都会一笔带过。他们只会讲RNN的梯度消失和梯度爆炸会影响SGD optimizer对参数的更新，从而引出不存在这两种问题的GRU和LSTM。但我认为这部分的推导是整个RNN最高难最有趣的地方。仔细研究一下不仅能让你复习很多忘掉的数学，还能对RNN的运行过程有更深刻的理解。

这里我会用上面介绍的第一种RNN来作为例子求梯度。

我们要求的梯度，就是当前的总损失对参数的梯度。求导的过程要用到我之前两个专栏的内容

所谓backward propogation，就是逆着unfolded computational graph箭头方向求导的过程。从图中我们能看出来，想对参数求梯度，是必经之路，所以我们先尝试求一下总损失对的梯度，进而对的梯度。下一步再求解或对这5个参数的梯度。

假设RNN已经训练到了时间，那么当前的总损失就是

对的梯度可以写成

这个用到了之前说过的链式法则。只要我们有关于梯度输入和输出维度的规定，梯度的链式法则和求导的链式法则是一致。在等号右边的三个梯度中，第一个根据上面的总损失公式就等于1；第二个需要求一个Vector-to-scalar函数的梯度，因为和的函数关系不涉及矩阵运算，我们只能用梯度的定义来求。之前我们假设我们的RNN用的是交叉熵损失函数cross entropy loss function，再假设RNN的输出是n维列向量，因此；

第三个是求一个Vector-to-vector函数的梯度，我们需要求的是Jacobian矩阵。和的关系是softmax函数，即

Jacobian矩阵的第i行j列可以表示为

所以的计算实质上是一个的梯度向量乘以一个的Jacobian矩阵

我们现在成功获得了在上面的梯度，下一步就可以求在别的参数上的梯度了。

我们先来看, 只从上面遗传下来。因为RNN中有明确的关于的矩阵表达式，所以我们可以用之前学过的Vector-to-vector求梯度的方法来计算：

所以

但是问题来了，是只从上面遗传下来，但是不是。从图中可以看出来，的传播方向不仅有，还有。所以为了链式法则能够连接到，我们需要找到在上的梯度

这个梯度的求解过程可以参考Quant 1.5里面的最后一个例子

因此我们能够得到关于梯度的迭代公式

我们逐步迭代，直到，我们就能获得关于梯度的确定的值。

所有的准备工作都做完了，我们现在获得了关于和的全部梯度，需要继续利用链式法则求的梯度：

多说一句以防大家忘记，这里的链式法则的情形比前面的要复杂一些。之前例子中的链式法则都是单链的，也就是说从复合函数的自变量变换到因变量的过程只有一个路径，但是在RNN中时间的存在使得到损失的变换在每一个时间都有一条平行的路径。多链的链式法则需要我们把每个平行路径的梯度加和来求总梯度。

然后上面我们已经求的了五个梯度中最简单的两个。但是在求另外三个的时候就会遇到一个问题...按照正常的链式法则，求关于的梯度的时候应该有

但是根据我目前学到的知识，这个我是算不出来的，因为是一个Matrix-to-vector函数的梯度，首先它的梯度求出来应该是一个三维tensor的形式，其次即使它的梯度有矩阵的表达形式，但是我认为这种表达形式放入chain rule进行计算是错误的。因此，上面的梯度无法这么求。

那我们应该怎么办呢？我们虽然不确定Matrix-to-vector函数的梯度能不能插入链式法则里面，但是我们能确定Matrix-to-scalar函数肯定是可以的！那我们可以不可以修改一下路径，使得由到的梯度变成Matrix-to-vector函数的梯度呢？可以！我们只要把的每一项拿出来作为中间项过度就可以了。大致变化差不多下面这张图，需要把展开：

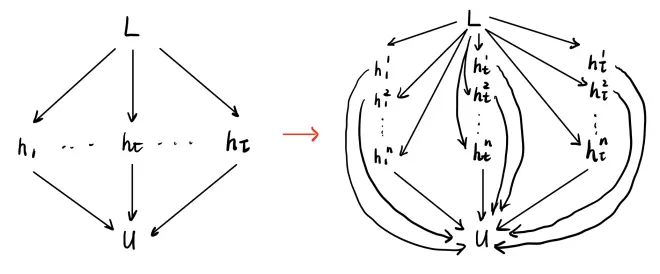
最后按照右边的图片，关于U的梯度就变成了

接下来是全篇最蹩脚的地方：如何化简上面的等式？首先我们要求一个Matrix-to-scalar函数的梯度

这个就不是很好理解。我们先看一下矩阵变换到的过程：第一步对于矩阵U进行线性变换，对得到的向量只保留第i项，第二部是。所以根据链式法则：

关于后面这个Matrix-to-scalar函数的梯度，因为这个函数里面的没有trace，所以我们只能通过Matrix-to-scalar函数梯度的定义来理解了。因为我们最后只取向量的第i项，所以矩阵U只有第i行和有关系。将对矩阵的第行各项求导，得到的就是向量每一项。因此，得到的梯度矩阵除了第i行是以外，其余项都是0。

下一步依然是难理解的一步，我们想要取消内部的求和符号就需要把所有关于都加起来：

所以

如果线代学的不是特别好的话，从求和符号到矩阵乘法之间的转换可能需要比较长的时间消化，这里大家可以多总结一下。

然后关于矩阵的梯度和U十分类似，我就不再推一遍了

梯度求完了，我们现在要讨论的是梯度为什么会消失 (gradient vanishing)，梯度又为什么会爆炸 (gradient exploding)。我在网上能找到的所有视频关于这两点都是泛泛而谈，包括上面的教材和视频，没有一个解释的很详细的，我感觉很无语。所以这里试着解释一下：

我们从上面一系列的梯度的推导中可以看出，每一个time step对参数的梯度都是有贡献的。但是如果我们的神经网络深度足够大的话，早期的time step对梯度的贡献会过小或者过大。这就是梯度消失/爆炸。

难道早期的time step对梯度的贡献小不是应该的吗？不一定！吴教授的视频中举了一个例子，假如我们现在想要预测一句不完整的话的下一个词是什么：

The cats, which already ate, were full.

The cat, which already ate, was full.

我们在预测这个was/were的时候，最重要的参考信息不是中间的非限制性定语从句，而是前面的cat/cats。因此，模型参数应该在cat/cats这个词对应time step的hidden state上面的梯度很大，从而可以显著的修改神经网络中的矩阵参数。然而，如果这个cat/cats离was/were太远了，这个梯度就会产生爆炸或者消失，导致我们最后训练出来的神经网络参数没有预测价值。毕竟语法上非限制性定语从句可以无限长。

那么如何从梯度的公式上理解梯度消失和梯度爆炸呢？根据我们之前推导过的梯度公式，可以知道损失函数关于各个矩阵/向量参数的梯度大多与有关系，而还有递推公式：

我们多写出来一步

这是两个time step的递推公式，我们可以知道当time step的间隔足够大的时候，多个矩阵会累乘到一起作为晚期time step梯度的系数。这就导致早期的time step梯度受矩阵的影响很大。就像是和差距很大一样，梯度下降的进程会受参数初始化的影响，如果初始化太大会造成梯度爆炸，太小则会造成梯度消失。