[Series] Sum of Squares

2021-07-10 18:34 作者:AoiSTZ23 0人读过 | 我要投稿

By: Tao Steven Zheng (郑涛)

【Problem】

In his work "On Spirals", Archimedes (287 – 212 BC) derived the formula for calculating the sum of consecutive perfect squares. Figure 1 shows the geometric representation of the sum

$1%5E2%2B2%5E2%2B3%5E2%2B4%5E2%2B5%5E2$

used by Archimedes. He was able to derive the formula

$%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%20k%5E2%20%3D%5Cfrac%7Bn(n%2B1)(2n%2B1)%7D%7B6%7D$

Explain Archimedes’ proof of the sum of consecutive perfect squares using modern algebraic notation.

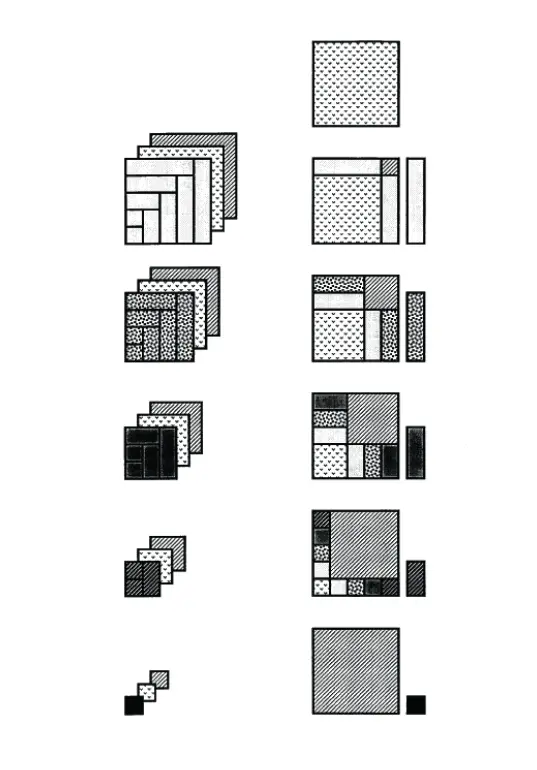
【Solution】

Figure 1 represents the equation

$3(1%5E2%2B2%5E2%2B3%5E2%2B%E2%8B%AF%2Bn%5E2%20)%3Dn%5E2%20(n%2B1)%2B(1%2B2%2B3%2B%E2%8B%AF%2Bn)$

Since

$1%2B2%2B3%2B%E2%8B%AF%2Bn%3D%5Cfrac%7Bn(n%2B1)%7D%7B2%7D$

it follows that

$3(1%5E2%2B2%5E2%2B3%5E2%2B%E2%8B%AF%2Bn%5E2%20)%3Dn%5E2%20(n%2B1)%2B%5Cfrac%7Bn(n%2B1)%7D%7B2%7D$

$3(1%5E2%2B2%5E2%2B3%5E2%2B%E2%8B%AF%2Bn%5E2%20)%3Dn(n%2B1)(n%2B%5Cfrac%7B1%7D%7B2%7D)$

$1%5E2%2B2%5E2%2B3%5E2%2B%E2%8B%AF%2Bn%5E2%3D%5Cfrac%7Bn(n%2B1)(2n%2B1)%7D%7B6%7D$

Consequently,

$%5Csum_%7Bk%3D1%7D%5E%7Bn%7D%20k%5E2%20%3D%5Cfrac%7Bn(n%2B1)(2n%2B1)%7D%7B6%7D$

标签：

[Series] Sum of Squares

By: Tao Steven Zheng (郑涛)

【Problem】

【Solution】