[翻译]锥线几何(Geometry of Conics)第一章:二次曲线的诸基本性质1.5

本文译自A. V. Akopyan, A. A. Zaslavsky, trans. Alex Martsinkovsky, Geometry of Conics, American Mathematical Society, 2007.
翻译:野吕侯奈因
仅供学习交流使用
译者按:
本书在几何爱好者之间小有人气,但目前网上只能找到一些零散的翻译.鉴于目前通行的数学教学中对于二次曲线问题的处理方式过于单一,希望能借翻译本书的机会来推广一下二次曲线的射影几何视角.

1.5. 作为圆的投影存在的二次曲线
给定一个圆,作出一条过其圆心并垂直于该圆所在平面的直线并于其上取一点.那么连接
与圆周上的所有点就会构成一个圆锥.考虑一个以不与轴线垂直的平面
截圆锥的截面其与母线的全部交点.
接下来作出该圆锥的两个内切球其切于点
和
(图1.20).

设为圆锥面与平面
的相交部分上任意一点,母线
交两内切球于点
和
.则有
与
,由于从球外一点引球的两条切线长度相等,有
.其中
为圆锥中垂直于轴线的两平面截母线所得线段,其长度不因
的选取而改变.因此圆锥面与
的相交部分即为椭圆.而两半轴间的比值由平面的倾斜程度决定并且显然可以取任意值.故任何椭圆都可以用圆的投影作出.
可以相似地证明一个平行于圆锥的两母线的割面,其截圆锥面所得图形为双曲线(图1.21).

最后,考虑当割面只平行于一条母线的情况(图1.22).
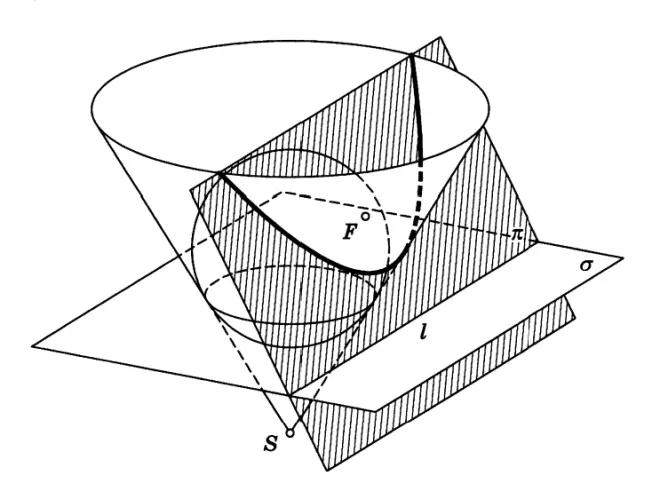
设圆锥的内切球切于点
,该球切圆锥于平面
上的一圆,而
为平面
与
的交线.对于圆锥面与平面
的相交部分上任意一点
,设
为母线
与平面
的交点,
为
在
上的投影,于是由切线长定理就有
.另外,
和
都落在
上,
与
的夹角等于
与
的夹角,而与
的选取无关.而由两线段与
间成角相等,有
.故有
,即
落在一条以
为焦点,
为准线的抛物线上.
于是所有非退化的二次曲线都可以用圆锥的截面作出,因此,这些曲线也被称做圆锥截面线(conic section)或圆锥曲线(conic).
我们注意到若将圆锥换成一个圆柱,经由同样步骤得到的截面就会变成椭圆.故椭圆也可以由圆的平行投影作出.
练习1. 试求椭圆中平行于某一方向的弦其中点轨迹.
解答. 考虑一个由平行投影作出的椭圆.则椭圆中平行弦中点就会对应于圆中平行弦中点,而后者会落在圆的直径上,故椭圆中弦中点的轨迹也会落在其直径上(即过其中心的弦).
练习2. 如何用直尺和圆规作出给定椭圆的两焦点.
解答. 首先作出椭圆中两平行弦.由上一题的结论,其中点所连直线为椭圆直径.再作出另一直径,便可以确定椭圆中心.由椭圆的对称性,以
为圆心作适当直径的圆,会交椭圆于构成分别与椭圆的两轴平行的矩形的四点.故可以作出一以短轴的一端点为圆心,半长轴长为半径的圆,而其与长轴交点即为焦点.
像这样在圆锥中与割面相切的内接球被称作丹迪林双球(Dandelin spheres).

