【高等数学（下）】2022 通关速学 第4章 曲线积分 曲面积分

第四章 曲线积分 曲面积分

曲线积分（第一类曲线积分）

物理意义：求密度不均匀的弧的质量

判断是几重积分，是看有几个积分符号的

例一：

如图为一元积分

关键：需要把不会算的ds换成能算的dx

例二：

这里没有ds，不用对弧长积分了，所以只需把dy换成dx即可

记得确定上下限

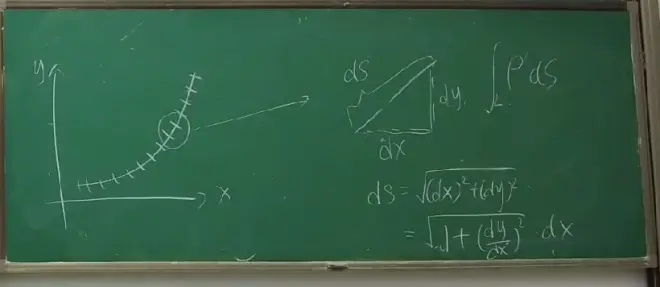
↑关于ds为什么换成根号下（1+y’²）

第一类曲线积分不带方向的原因：

第一类曲线积分：

1.对x积分 把dy（或ds）换成dx

2.对y积分 把dx（或ds）换成dy

3.对t积分 把dx和dy换成dt

曲线积分（第二类曲线积分）

物理意义：求力沿某一弧长运动的做功（所以带方向）

其他与第一类曲线积分一样

格林公式

格林公式如图↑

粉色圈圈所做的功之和与外面百环的做功相等

所以：一个闭环的做功等于把这个闭环划分为无数个小环做功之和

如下面这个网格↓

这里（天意学长手指的位置）的意思应该是f（y）也就是y方向上的力随着dx增加或者减少，也就是两个力相减

格林公式作用：

格林公式可以验证某一曲线积分与路径无关（要求：格林公式的被积函数等于0）

曲面积分（第一类曲面积分）

例题：

把所求面投影到xoy平面上

然后通过投影面（闭环）找到x和y的上下限

最后把ds改成关于dxdy的样子，记得把被积函数中z的部分替换成关于x和y的式子

（ds与dxdy的关系↑）

曲面积分（第二类曲面积分）

（物理意义：流体通过某一曲面的流量）

怎么判断是第一类还是第二类

式子很直白的给你dx，dy，dz的就是

第一类曲面积分给的是ds

根据三视图分别处理dxdy，dxdz，dydz

注意替换变量时的正负号

二重积分的区间是一个封闭区域，所以没有围成一个封闭图形的二重积分为零