书接上回。

上一期我们构建了概率的基本理论，这一期就介绍一些我们在运用概率知识时常见的情况。

当然，介绍前我们需要先有一点前置知识。

1.随机变量

我们之前用集合的形式表示了随机事件。但是数学数学我们还要把它与数扯上联系。

因此我解决实际问题时我们还要建立事件和数的一一对应关系。

这个就是所谓的随机变量了。

因此之后我们便可以利用随机变量来研究某个事件发生的概率了。

2.离散型随机变量及其概率分布

有一些随机变量例如摸到黄球的个数只可能是一些离散的自然数，这类随机变量称为离散型随机变量。描述它的概率分布只需要直接列一个表格(称为分布列)就好了。

我们在表格的第一行写上随机变量可能取的值，第二行写上相应的概率就得到分布列了。

例如这张就是某个随机变量的分布列

当然，除了用分布列之外还可用表达式来表示。

对于前面举的那个例子，我们可以用表达式把随机变量取-2,-1,0,1,2,3的概率都表达出来。

下面我们的讨论更多地会使用这种方式。

3.连续型随机变量及其概率分布

还有一类随机变量比如你家电灯剩余的使用寿命，它可能的取值不是一些离散的数。

这类随机变量我们称为连续型随机变量吗？

不对！

这个只是我们朴素的理解而已。基于这个朴素的理解人们便想到了用概率密度函数来描述它飞概率分布。然而概率密度函数却存在漏洞。为了填补这个漏洞

数学上定义：

如果某个随机变量X满足

存在一个非负函数使得，则称X为连续型随机变量。

其中f(x)称为X的概率密度函数，简称概率密度。

这里的定义并不能保证所有取值在某个区间的函数都满足。

比方说，当你试图找某个随机变量的概率密度的时候发现它不可积，那么这个随机变量就不是连续型随机变量了。

对于这种及特殊的个例我们就直接引入了概率分布函数来解决。

不管哪个随机变量，函数总是存在的，我们称这个函数为随机变量X的分布函数。

而我们后面讨论的比较多的是连续型随机变量的概率分布。

对于连续型随机变量我们可以不用概率分布函数而使用概率密度函数。

这是因为当你试图求随机变量在某个区间[a,b]上的概率时，可以这样得到

也就是说，求某个区间上的概率只需要对概率密度求积分就行了。

什么？你问我开区间怎么办？

没事的。区间开不开不影响答案因为连续型随机变量取单点的概率为0。

这个结论似乎有点反人类？

连续型随机变量是可能取某个特殊点的吧。但是取这个特殊点的概率为零。

概率为0的事件可能发生，概率为1的事件（概率为0事件的补事件）也有可能不发生。

例如，在[1,2]上等可能地随机找一点，它刚好是1.5的概率就是0（几何概型嘛）。

那么它的补事件，这个点刚好不是1.5的概率就是1了。

注意哦，我们的公理化体系只保证了发生的概率是1，发生的概率是0。

事件能推概率，但是概率推不了事件。

不过我凭啥说连续型随机变量取单点的概率为0呢？

首先，连续型随机变量的概率密度函数f(x)是可积的，这也就意味着其变上限积分函数（概率分布函数）F(x)是连续的。

然鹅我们有，

因而当时，不等号右边也趋于0。

概率的有界性又说任何概率都大于等于0。

因此X取a的概率就等于0啦。

这样的话单点取不取根本不会影响整个区间的概率。

注意注意，概率密度函数什么的都是定义在R上的。如果随机变量不可能落在那个区域，则这个区域上的概率密度函数函数值为0。

下面为了简便，函数值为0的区域我不会写出。

概率密度函数不一定要用f(x)表示，比如我后面会用P(x)表示(只是这篇刻意这么做来消除偏见而已，以后回归正常)

4.超几何分布

理论铺垫完毕，这下可以拿它解决实际问题喽。

先从我们说了好几次的摸球开始吧。

我们假设不透明的箱子里放了N个球，其中有N1个黄球，N2个绿球，并且这些球除了颜色外没有任何区别。现在你随机从里面摸出n个球，问取到黄球的数目X的概率分布。

这里就是一个典型的古典概型问题了。

先来看X可能取几吧。（额，说几不说吧，文明你我他）

显然X可能取1,2,3......min{n,N1}

停停停，你这min是什么鬼？

一共就N1个黄球吧，所以你拿的黄球数不会超过N1。

一共就拿n个球，所以你拿的黄球数也不会超过n。

就这个意思而已。

现在只要求出X取k的概率就ojbk了。

这个不难求，，其中k+l=n。(额，这么写是因为B站的公式编辑器只能这样显示，下面上图片）

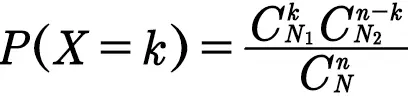
我来解释一下，分母是从N个球里选n个球的所有可能数。

分子分两步。

第一步从N1个黄球里选k个黄球。

第二步从N2个绿球里选l个绿球。

这样就是实现X=k的全部可能数。

一般地，上面这种概率分布我们称为超几何分布。

我们用符号X~H（n，M，N）表示X满足超几何分布。n,M,N表示从N个样本(如球）里取n个样本，其中有M个样本具有某种特性（如黄球）

超几何分布的

期望是nM/N

方差是nM(N-n)(N-M)/N²(N-1)

(期望方差不知道什么意思的可以等之后介绍)

5.几何分布

在

这篇专栏里我介绍了几何分布。

在这里说一句只是因为名字和超几何分布有点像而已hh。

几何分布的期望是1/p

方差是根号(1-p)/p

6.二项分布

按照正常的逻辑这里应该说二项分布才对。

二项分布是这样的。

假设你从口袋里摸出黄球的概率是p，并且你每次都把球放回去。

求你重复摸n次后拿到黄球的个数X的概率分布。

这个超级简单。

X可能取1,2,3，......，n

而其中k+l=n

即

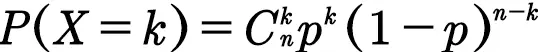
式子的组合数表示你有多少种不同的拿法。（比如前k次全是黄球后面全是其他球）

P的k次方就是说你成功了k次的概率。(1-p)的l次方则是失败的概率。

这样的概率分布称为二项分布。

X满足二项分布记作X~B(n，p）。n，p表示重复n次，每次成功的概率是p。

二项分布的期望是np

方差是np(1-p)

7.0-1分布

0-1分布是二项分布的特例即n=1的情况。即只进行一次试验，成功的概率是p。

X满足0-1分布你可以沿用二项分布记作X~B（1，p）你也可以把1省略变成X~B(p)

0-1分布是二项分布n取1的特殊值所以期望是p，方差是p(1-p)

8.泊松分布

接下来的玩意就是各位高中生不能免费听的付费内容了。(笑)

请问成华大道在某一段时间的车流量X满足什么概率分布？

这个上手就比较难了。

所以我直接来喽。

我们可以用微积分的思想把这段时间分割了（经典的分割近似求和取极限）。

只要我们把这段时间分割得足够细，那么在每一小段时间里就只有一辆车或者没有车通过了。

这时情况不就变成了我们熟悉的二项分布了。

我们将时间分割成了n次，假设每次有车经过的概率是p

当n趋于+∞时我们的分割近似就是准确的了。

这样车流量为k的概率就是

即

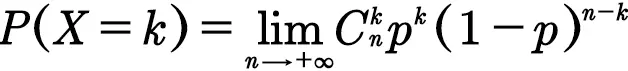
我们是在聊概率，这个算极限的过程我就不说了。

具体步骤如下

上面这个呢就是泊松定理，最后随机变量的概率分布（那坨带λ的式子）就是泊松分布了。

它指出二项分布的极限情况就是泊松分布。

反过来我们也可以用泊松分布近似替代二项分布（毕竟二项分布不好算嘛）。

一般地X满足泊松分布记作

X~P(λ)，这里的λ就是刚刚式子里的那个。

泊松分布的期望与方差都是λ。

9.伽马分布

泊松分布再往后延伸就是伽马分布了。

如果事件A服从泊松分布(其实任意分布都可以)，那么等到这件事第k次发生的时间间隔t服从的就是伽马分布了。记作t~Ga(k，λ)

对了，你也看到了。这篇专栏已经有点太长了，所以后面的一些推导和计算我就不说了。

总之，伽马分布的概率密度函数是(注意，时间间隔是连续的)

分母那个是伽马函数。

t作为时间间隔不可能为负数。

在上面的式子里，t是时间间隔，k称为形状参数，λ为逆尺度参数。

伽马分布的期望是k/λ，方差为k/λ²

10.指数分布

伽马分布的一个特例就是指数分布。

即事件A第一次发生需要的时间间隔。取k=1即可得到

同样，在这里t作为时间间隔不可能为负数。

你可以记t满足指数分布为

t~Ga(1，λ)

也可以用它的专有记号

t~Exp(λ)

指数分布的期望是1/λ，方差为1/λ²

11.均匀分布

连续型随机变量的概率分布里最简单的是均匀分布。

这个很简单，就是字面意思。

即随机变量X在区间[a，b]上等可能分布，且X不可能落在区间外。

记作X~U(a，b)

其概率密度函数为

期望为

方差为

12.拉普拉斯分布

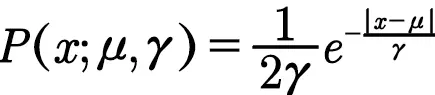
其中μ为位置参数，γ为尺度参数。

X服从拉普拉斯分布记作

X~La(μ，γ)

它的期望是μ

方差是2γ²

13.贝塔分布

前面提到了伽马函数那自然就有它的好兄弟贝塔函数相关的分布啦。

但是贝塔分布的变量只可能取(0，1)的值。

如果X服从贝塔分布即X~Be(α，β)

则其概率密度为

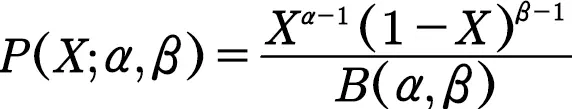
其期望为α/(α+β)

方差为αβ/(α+β)²(α+β+1)

14.正态分布

正态分布又称高斯分布、常态分布。它是一个非常重要的概率分布，我们之后还会遇到它。

如果随机变量X服从期望为μ，方差为σ²的正态分布记作X~N(μ，σ²)

当μ=0，σ=1时的正态分布我们称为标准正态分布。

一般地我们有，

若X~N(μ，σ²)，那么~N(0，1)

这个就是正态分布的标准化。

标准化意味着要算正态分布的概率只需要计算其对应的标准正态分布的概率即可。

而标准正态分布的概率我们一般直接查表获得。（当然，现在其实更建议利用计算机解决）

正态分布的概率密度函数是

当然，既然可以标准化一个正态分布，所以其实这个一般情况是不太用的上的。顶多标准正态分布的用的上一点而已。

这个概率密度函数是这样的一个两头低，中间高且左右对称的钟型曲线。

这张就是标准正态分布的概率密度函数的图像。

你看，是不是确实有点像。

15.柯西-洛伦兹分布

这个分布其实不常见但是它有一个特殊的地方。

这个分布的期望和方差以及高阶矩都不存在。

X服从柯西-洛伦兹分布记作X~C(γ，x0)

其概率密度函数为

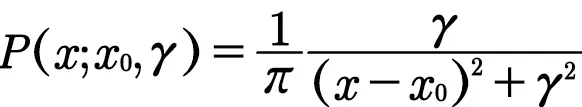
当γ取1，x0取0时的特例我们称为标准柯西分布。

其实还有很多概率分布我没说，比如狄拉克分布、狄利克雷分布、多项式分布等等。想了解的话就自己上网查阅吧。这里已经罗列了太多了。