【经济学基础Ep5】范里安《微观经济学:现代观点》概念梳理P34:效用

(合计2750字,用时160min——)
4 效用
概念——
效用:
作用:效用仅仅看作是描述偏好的一种方法;
定义:对消费束(x1,x2)的偏好超过对消费束(y1,y2)的偏好,就意味着消费束X的效用大于消费束Y的效用;
效用函数:
含义:为每个可能的消费束指派一个数字的方法,它指派给受较多偏好的消费束的数字大于指派给受较少偏好的消费束的数字;
特征:效用指派的唯一重要特征在于它对消费束所进行的排序——
效用函数的数值,只在对不用消费束进行排序时才有意义;
任意两个消费束之间的效用差额的大小是无关紧要的,
因为这种效用强调消费束的排列次序,所以它被称作序数效用。
单调变换:
含义:单调变换是以保持数字次序不变的方式将一组数字变换成另一组数字的方法;
方式:用把每个数字u转换成其他某个数字f(u)的函数f(u)来表示一个单调变换;
性质:单调变换和单调函数在本质上是同一回事;
例子:
乘以一个正数;
加上任意数;
u的奇次幂;
测度:通过考察两个u值之间的f的变动除以u的变动的商,可以测度随u变动的f(u)的变动率——

——对于单调变换来说,f(u2)-f(u1)同u2-u1的符号始终是一样的,
——因此,单调函数的变动率总是正的。
规律:
内容:如果f(u)是表示某种偏好的效用函数的任一单调变换,那么f(u(x1,x2))就一定也是一个表示那些相同偏好的效用函数;
原理:一个效用函数的单调变换还是一个效用函数,这个效用函数代表的偏好与原效用函数代表的偏好相同;
命题:

4.1 基数效用
概念:
含义:有一些效用理论对效用的数值赋予了重要意义,这些理论被称作基数效用理论——在这种理论中,两个消费束之间的效用差额的大小被认为具有某种重要的意义;
局限:既然基数效用并不是描述选择行为所必需的,而且,也没有任何令人信服的方法来指派基数效用,所以我们将完全坚持序数效用的分析框架。
4.2 构造效用函数
方法:
我们知道,效用函数是一种为无差异曲线标记数字使得受较多偏好的无差异曲线得到较大数字的一种方法;
一种容易的做法是画一条对顶线,沿着这条线测度每条无差异曲线离原点的距离,并以此标记每条无差异曲线;
不难看出,如果偏好是单调的,这条经过原点的直线就一定与每条无差异曲线只相交一次——
因此,每个消费束只能标记一个数字,而且,处在较高位置的无差异曲线上的那些消费束将标上较大的数字——这一切表明这就是一个效用函数。
结论:几乎任何一种“合理”的偏好都能够用效用函数表示。
4.3 效用函数的几个例子
概念:使得u(x1,x2)等于一个常数的所有点(x1,x2)的集合称作水平集。
a.例子:由效用推导出无差异曲线
前提:假设效用函数由u(x1,x2)=x1x2给出——
例子1:

——将x2作为x1函数求解,满足公式x2=k/x1
——画出k=1,2,3,…时的无差异曲线;
例子2:

——效用函数v(x1,x2)是原先效用函数u(x1,x2)的单调变换,
——这意味着v(x1,x2)的无差异曲线与u(x1,x2)的无差异曲线的性质完全相同,
——无差异曲线上标记的数字有所不同——原先是1,2,3,...现在变成了1,4,9,...
——v(x1,x2)=9的消费束的集合与满足u(x1,x2)=3的消费束的集合完全相同
——因为v(x1,x2)和u(x1,x2)以完全相同的次序对全部消费束进行排列,描述同一偏好。
方法:
数学方法:已知无差异曲线,我们要找到这样一个函数,沿每条无差异曲线它都是一个常数,并且对较高的无差异曲线指派较大的数字;
直观方法:假定已知对偏好的描述,我们要尽量考虑消费者在试图使什么实现最大化——哪一种商品组合能描述消费者的选择行。
b.完全替代
效用函数:
1比1完全替代:
函数1:u(x1,x2)=x1+x2;
函数2:u(x1,x2)=(x1+x2)^2;
不同于1比1的比例换取:u(x1,x2)=ax1+bx2——这里的a和b是用来测度商品1和商品2对于消费者的“价值”的某两个正数,典型的无差异曲线的斜率由-a/b给出。
c.完全互补
效用函数:
1比1完全替代:u(x1,x2)=min{x1,x2};
不同于1比1的比例换取:u(x1,x2)=min{ax1,bx2}——式中的a和b是描述商品消费比例的正数。
d.逆线性偏好
图线:
做法:假设消费者的无差异曲线都是相互之间垂直平移得到的;
效果:全部无差异曲线都是一条无差异曲线垂直“移动”的效果;
结论:无差异曲线的方程一定采取x2=k-v(x1)的形式,其中k是对不同的无差异曲线取不同的值的常数;
规律:
每条无差异曲线的高度等于x1的某一函数-v(x1)再加上常数k;
较高的无差异曲线的k值较大;
减号只是为了方便,下面我们就会明白为什么用减号比较方便;
这里自然用k来为无差异曲线标号——大致来说,k就是无差异曲线在纵轴方向的高度;
并解k并令它等于效用;
效用函数:u(x1,x2)=k=v(x1)+x2;
含义:效用函数对商品2来说是线性的,但对商品1来说却是非线性的——因此,它称作拟线性效用,意味着“局部线性”的效用;
例子:
函数1:
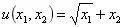
函数2:

e.柯布-道格拉斯偏好
柯布-道格拉斯效用函数:
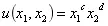
说明:
c和d都是描述消费者偏好的正数;
地位:柯布-道格拉斯偏好是良态无差异曲线的标准范例,
意义:事实上,描述它们的公式大约就是产生良态偏好的最简单的代数表达式;
例子:
函数1:取效用的自然对数,各项的乘积就会变成相加的和,因此我们就会有——

——由于取对数是一种单调变换,所以
——这个效用函数的无差异曲线看起来就像最初的柯布-道格拉斯函数的无差异曲线。
函数2:

——我们总是能够对柯布-道格拉斯效用函数作单调变换而使指数和等于1。
4.4 边际效用
边际效用:
含义:考察这样一个消费者,他(或她)正在消费某消费束(x1,x2),当我们稍微给他(或她)一点商品1时,这个消费者的效用的变化率;
公式——
边际效用:
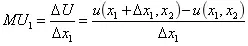
——它测度与商品1数量的微小变动(Δx1)相联系的效用变动(ΔU)率,
——商品2的数量在此计算中保持不变。
效用变动:

——为了计算同商品1的消费的微小变动联系在一起的效用的变动,我们只需要
——使消费的变动量乘上这种商品的边际效用。
4.5 边际效用和边际替代率
边际替代率(MRS):
应用:效用函数u(x1,x2)可以用来度量边际替代率(MRS);
几何分析:边际替代率度量的是给定消费束上的无差异曲线的斜率——它可以被解释为消费者恰好愿意用商品2代替商品1的比率;
意义:这种解释使我们得到一个计算边际替代率的简单方法;
方法:考察在效用保持不变的条件下每种商品的消费的变化(Δx1,Δx2)——即我们沿着无差异曲线移动时消费的变化,那么一定有

4.6 通勤车票的效用
一种形式:

其中:
TW=乘公交车或自己驾车要用的全部步行时间;
TT=以分钟计算的全部行车时间;
C=以美元计算的全部行车费用。

