Cox回归模型(Cox regression model)是生存分析最常用的一种方法，由于其原理的简单性、参数的易解释性，且对生存时间无分布形式的要求，自从1972年由D. R. Cox提出以来，被广泛应用于“时间-事件”数据(time-to-event data)，也是生存资料多因素分析的基本方法。其基础模型要求生存资料满足比例风险(Proportional Hazard)假定，故又称为Cox比例风险回归模型(Cox proportional hazards regression model)。

目录：

一、什么是PH假定？

二、PH假定的检验方法

（一）KM曲线法

（二） Schoenfeld残差图法

（三）累计鞅残差图-Supremum检验法

（四）构建协变量与时间的交互项

三、总结

一、什么是PH假定

  首先，我们要了解Cox风险比例回归模型的一般表达式：

其中，

t：生存时间；

X：协变量X1、X2、…、Xm向量；

h(t, X)：具有m个协变量的个体在t时刻的风险函数，即生存时间已经达到t的个体在t时刻的瞬时风险率；

h0(t)：基准风险函数，指t时刻所有协变量取值全为0时的风险函数。由于在模型估计过程中其可以被消去，因此允许其未知，也可以不对其分布做任何假定；

h(t, X)/h0(t)为风险比HR(Hazard Ratio, HR)，其对数与协变量之间呈线性关系，

β1、β2、…、βm：模型中的待估参数，为各协变量的偏回归系数，含义为其他协变量不变的情况下，协变量Xm每变化一个单位，其对数风险比的平均改变量。

比如，对于只含有一个二分类变量X1的情形，X1=1表示暴露于某因素，X1=0表示未暴露于某因素，此时模型可表达：

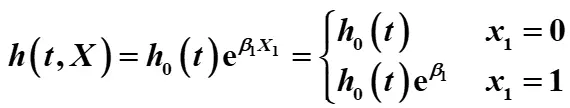
  则暴露的相对风险比为：

  显然，不论基线风险如何，在基线以后的任何时间点上，分别在影响因素的“暴露水平”与“非暴露水平”条件下的发生事件的风险比是恒定的。换句话说：影响因素的“暴露水平”与“非暴露水平”条件下的发生事件的风险比在整个随访期间是恒定的，与基准风险函数h0(t)无关，也与时间t无关，即模型中自变量的效应值不随时间而改变，称为比例风险(Proportional Hazard)假定，简称PH假定。

二、 PH假定的检验

包括图示法和假设检验法两类，常用方法包括：

（一）KM曲线法：针对协变量为定性变量

（二）Schoenfeld残差与log(t)的关系图法：协变量为定量变量或定性变量

（三）累计鞅残差图-Supremum 检验法：协变量为定量变量或分类变量

（四）构建协变量与时间的交互项

 

（一）KM曲线法—适用定性协变量的PH假定的检验

通过绘制定性变量各水平组的Kaplan-Meier 生存率曲线图(简称KM曲线)，如果不同水平组得KM曲线存在交叉，则表示该定性协变量不满足比例风险假定。另外，也可以通过绘制ln{-ln[S(t)]}与生存时间t或对数生存时间log(t)关系图，如果各组曲线明显不平行，说明该定性自变量不符合比例风险假设。KM曲线法是一种比较粗糙、主观的方法，而且即使不相交的曲线也可能不满足PH假定，因此一般用于PH假定的初步分析。

SAS代码：

proc lifetest data=Myeloma plots=(survival(cb=hw test atrisk(outside maxlen=13)) LLs);

        time Time * VStatus(0);

        strata platelet;

run;

 

关键代码：

plots=(survival(cb=hw test atrisk(outside maxlen=13))LLs)

其中：

cb：显示生存函数的置信带（即不同时刻的置信区间）。默认值为CB=HW，即显示Hall-Wellner 置信带。

Test：显示 STRATA 语句中指定的log-rank检验的P值。

LLs：LOGLOGS的简写。绘制估计幸存者函数的负对数对数与时间对数的关系图。

 

结果：

两组KM曲线和关系图不存在交叉基本平行，可以认为满足PH假定。

（二）Schoenfeld残差图法—定性、定量自变量通用

  该方法通过绘制Y轴为每个协变量的缩放Schoenfeld残差，X轴为对数生存时间log(t)的Schoenfeld残差图实现。若满足等比例风险假设，则该协变量下的Schoenfeld残差随时间围绕0上下波动，且拟合曲线与X轴基本平行，其斜率接近0，即Schoenfeld残差与时间不存在相关性。同时，zph检验通过考察Schoenfeld残差与时间的相关系数是否为0也进一步说明了等比例风险假设。

该方法应用广泛，对定性和定量资料都适用。

SAS代码：

PROC PHREG data=Myeloma zph(global transform=log) ;       CLASS  platelet frac;

        MODEL time*vstatus(0)=LogBUN HGB Platelet Age LogWBC Frac LogPBM Protein Scalc/ selection=s;

RUN;

 

关键代码：

zph(global transform=log)

其中：

zph：请求基于加权残差的诊断，以检查比例风险假设。

global：计算全局相关性测试。

结果：

首先看zph检验结果，最下面一行全局假设(_Global_）的P=0.0351，P<0.05说明模型中有变量不满足PH假定，改变量为LogBun。

变量LogBun的Schoenfeld残差图显示，拟合曲线和X轴不平行，可以认为不满足PH假定。

变量HGB的Schoenfeld残差图也显示，拟合曲线和X轴基本平行，满足PH假定。

（三）累计鞅残差图-Supremum检验法——定性、定量协变量通用

该方法通过绘制各变量的对数生存时间-累积鞅残差图，同时模拟若干条模拟数据的路径图，若实际路径图在模拟路径图的范围内，则可认为满足等比例风险假定。此外，还可以通过“Kolmogorov-Type Supremum”检验（简称Supremum检验）进行等比例风险假定进行假设检验。Supremum检验通过对若干条（通常为1000条）路径与实际路径进行比较得出P值，若P≤α则认为不满足等比例风险假定。

SAS代码：

PROC PHREG data=Myeloma ;

        CLASS  platelet frac;

        MODEL time*vstatus(0)=LogBUN HGB Platelet Age LogWBC Frac LogPBM Protein Scalc/ selection=s;

        Assess var=(LogBUN) ph /seed=222 resample=1000;

       

RUN;

关键代码：

Assess ph /seed=222 resample=1000;

ASSESS：要求进行Cox回归模型的充分性检验。通过这个语句，可检验一个或多个协变量的函数形式。PH选项要求进行比例风险假设。

Resample 选项即要求 SAS进行1000次模拟计算，并根据模拟计算结果进行Supremum 检验。

Seed：指定抽样随机种子数。

 

结果：

图为对数生存时间-累积鞅残差路径图及Supremum检验示例，实线为实际累积鞅残差路径图，虚线为模拟数据的路径图，左下方Pr为Supremum检验所得P值。

变量HGB仍然满足PH假定(P=0.5510)，然而logBUN不满足PH假定(P=0.0490)。

（四）构建协变量与时间的交互项

将欲考察协变量和对数时间log(t)的以乘积交互项的形式纳入模型，若交互项的偏回归系数有统计学意义，则不满足PH假定。

PROC PHREG data=Myeloma ;

        CLASS  platelet frac;

        MODEL time*vstatus(0)=LogBUN LogBUNt HGB Platelet Age LogWBC Frac LogPBM Protein Scalc/ selection=s;

        LogBUNt=LogBUN*log(time);

       

RUN;

三、总结

推荐Schoenfeld残差图法和累计鞅残差图-Supremum检验法，其通过图示法与假设检验法相结合的形式使结果更为可靠，而且适用范围广泛，适用于定量或定性协变量，。

 

下期：PH假定不成立，我们该怎么解决？

R语言如何实现PH风险假设？

 

 

参考文献：

[1]Cox D R. Regression models and life‐tables[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1972, 34(2): 187-202.

[2]Grambsch P M, Therneau T M. Proportional hazards tests and diagnostics based on weighted residuals[J]. Biometrika, 1994, 81(3): 515-526.

[3]Lin D Y, Wei L J, Ying Z. Checking the Cox model with cumulative sums of martingale-based residuals[J]. Biometrika, 1993, 80(3): 557-572.

[4]Borgan Ø, Zhang Y. Using cumulative sums of martingale residuals for model checking in nested case‐control studies[J]. Biometrics, 2015, 71(3): 696-703.

 

文字编辑、程序编辑：天涯二毛君

审稿：老陈

关注微信公众号，获取更多相关内容！