By: Tao Steven Zheng (郑涛)

【Problem】

The bicylinder is a solid formed by intersecting two perpendicular cylinders of equal cross-sections. The cross-sections of the intersecting cylinders are circles of radius . Use integration to determine the volume of the bicylinder.

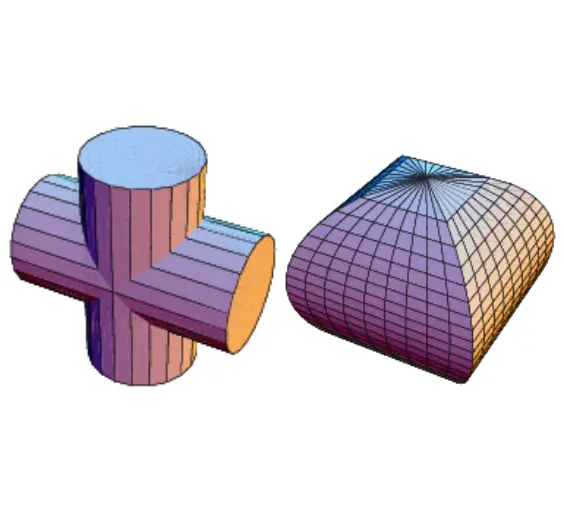
【Solution】

The first thing to consider are the level-curves in the direction of integration. Let the integration be carried out in the x-axis. The cross-sections in the x-axis are squares that vary under the constraint of a circle with radius , which is the circle . The side length the cross-sectional squares is given by the formula

Thus, the cross-sectional areas is the function

To determine the volume, integrate in the x-axis from one end of the circle to the other end.