a.基本简介

一般地，我们把形如y=ax²+bx+c（其中a，b，c是常数，a≠0）的函数叫做二次函数，其中a称为二次项系数，b为一次项系数，c为常数项。x为自变量，y为因变量。等号右边自变量的最高次数是2。

b.主要特点

“变量”不同于“未知数”，不能说“二次函数是指未知数的最高次数为二次的多项式函数”。“未知数”只是一个数（具体值未知，但是只取一个值），“变量”可在一定范围内任意取值。在方程中适用“未知数”的概念（函数方程、微分方程中是未知函数，但不论是未知数还是未知函数，一般都表示一个数或函数——也会遇到特殊情况），但是函数中的字母表示的是变量，意义已经有所不同。从函数的定义也可看出二者的差别.如同函数不等于函数关系。

折叠二次函数图像与x轴交点的情况

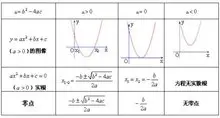
当Δ=b²-4ac>0时，函数图像与x轴有两个交点。

当Δ=b²-4ac=0时，函数图像与x轴只有一个交点。

当Δ=b²-4ac<0时，函数图像与x轴没有交点。

c.图像

在平面直角坐标系（Plane rectangular coordinates）中作出二次函数y=ax²+bx+c的图像，可以看出，二次函数的图像是一条永无止境的抛物线。 如果所画图形准确无误，那么二次函数图像将是由一般式y=ax²平移得到的。

注意：草图要有 :

1. 本身图像，旁边注明函数。

2. 画出对称轴，并注明直线解析式 （x= -b/2a）

3. 与x轴交点坐标 (x₁,0)，(x₂, 0)，与Y轴交点坐标(0,c)，顶点坐标[-b/2a, (4ac-b²)/4a].

d.轴对称

二次函数图像是轴对称图形。对称轴为直线x=-b/2a. 

对称轴与二次函数图像唯一的交点为二次函数图像的顶点P. 

特别地，当b=0时，二次函数图像的对称轴是y轴（即直线x=0）. 

当a,b同号，即ab>0时，对称轴在y轴左侧.

当a,b异号，即ab<0时，对称轴在y轴右侧.

e.顶点

二次函数图像有一个顶点P，坐标为P ( h,k )，即[-b/2a, (4ac-b²)/4a].

当h=0时，P在y轴上；

当k=0时，P在x轴上。

即可表示为顶点式y=a(x-h)²+k。

由一般式转化为顶点式：h=-b/2a， k=(4ac-b²)/4a。

f.开口方向和大小

二次项系数a决定二次函数图像的开口方向和大小。

当a>0时，抛物线向上开口；当a<0时，抛物线向下开口。

|a|越大，则二次函数图像的开口越小；反之，则二次函数图像的开口越大。

g.决定对称轴的因素

二次项系数a和一次项系数b共同决定对称轴的位置。

二次函数

当a>0，与b同号时（即ab>0），对称轴在y轴左侧。 因为对称轴在左边则对称轴小于0，也就是- b/2a<0，所以 b/2a要大于0，所以a、b要同号

当a>0,与b异号时（即ab<0），对称轴在y轴右侧。因为对称轴在右边则对称轴要大于0，也就是- b/2a>0, 所以b/2a要小于0，所以a、b要异号

可简单记忆为“左同右异”，即当a与b同号时（即ab>0），对称轴在y轴左侧；当a与b异号时（即ab<0 ），对称轴在y轴右侧。

事实上，b有其自身的几何意义：二次函数图像与y轴的交点处（即x=0处）的该二次函数图像切线的函数解析式（一次函数）的斜率k的值，即 f`(0)=b，可通过对二次函数求导得到。 

h.决定与y轴交点

常数项c决定二次函数图像与y轴交点。

二次函数图像与y轴交于(0,c)，即 f(0)=c

注意：顶点坐标为（h,k)， 与y轴交于（0,c)

i.

a<0且k>0或a>0且k<0时，二次函数图像与x轴有2个交点。

k=0时，二次函数图像与x轴只有1个交点。

a<0且k<0或a>0且k>0时，二次函数图像与x轴无交点。

当a>0时，函数在x=h处取得最小值ymin=k，在(h,+∞)范围内是单调递增，在(-∞,h]范围内是单调递减，二次函数图像的开口向上，函数的值域是[k,+∞)

当a<0时，函数在x=h处取得最大值ymax=k，在(-∞,h]范围内是单调递增，在(h,+∞)范围内是单调递减，二次函数图像的开口向下，函数的值域是(-∞,k]

当h=0时，抛物线的对称轴是y轴，这时，函数是偶函数

j.性质

定义域（domain）：R

值域：当a＞0时：①[(4ac-b²)/4a, +∞)；②[t, +∞)

当a＜0时：①(-∞, (4ac-b²)/4a]；②(-∞, t]

奇偶性：当b=0时，函数为偶函数；当b≠0时，函数为非奇非偶函数 。

周期性：无

解析式：

①y=ax²+bx+c [一般式]（a≠0）

⑴a≠0

⑵a>0，则抛物线开口朝上；

a<0，则抛物线开口朝下；

⑶极值点（顶点）：[-b/2a，(4ac-b²)/4a]；

⑷Δ=b²-4ac（判别式）

Δ>0，图象与x轴交于两点：

（[-b-√Δ]/2a，0）和（[-b+√Δ]/2a，0）；

Δ=0，图象与x轴交于一点：

（-b/2a，0）；

Δ<0，图象与x轴无交点；

特殊地，当Δ=4，顶点与两零点围成的三角形为等腰直角三角形；

当Δ=12，顶点与两零点围成的三角形为等边三角形。

②y=a(x-h)²+k [顶点式]（a≠0）

此时，对应极值点为（h，k），其中h=-b/2a，k=(4ac-b²)/4a

③y=a(x-x₁)(x-x₂) [交点式（双根式）]（a≠0）

对称轴X=(X₁+X₂)/2 当a>0 且X≧(X1+X2)/2时，Y随X的增大而增大，当a>0且X≤（X₁+X₂）/2时Y随X的增大而减小。此时，

x₁、x₂即为函数与X轴的两个交点，将X、Y代入即可求出解析式（一般与一元二次方程连用）。

交点式是Y=A(X-X₁)(X-X₂) 知道两个x轴交点和另一个点坐标设交点式。两交点X值就是相应X₁ X₂值。

增减性

当a>0且y在对称轴右侧时，y随x增大而增大，y在对称轴左侧则相反，同增同减。

当a<0且y在对称轴右侧时，y随x增大而减小，y在对称轴左侧则相反，大小小大。

最值

当a＞0时，函数有最小值（4ac-b²）/4a。

当a＜0时，函数有最大值（4ac-b²）/4a。

k.分类

一般式

y=ax²+bx+c (a≠0,a、b、c为常数)，顶点坐标为 [-b/2a,(4ac-b²)/4a]

把三个点代入式子得出一个二元一次方程组，就能解出a、b、c的值。

折叠顶点式

y=a(x-h)²+k (a≠0,a、h、k为常数), 顶点坐标为（h,k），对称轴为x=h，顶点的位置特征和图像的开口方向与函数y=ax²的图像相同，有时题目会指出让你用配方法把一般式化成顶点式。

例：已知二次函数y的顶点(1,2)和另一任意点(3,10)，求y的解析式。

解：设y=a(x-1)²+2，把（3，10）代入上式，解得y=2(x-1)²+2。

折叠交点式

y=a(x-x₁)(x-x₂) (a≠0) [仅限于与x轴即y=0有交点A（x₁，0）和 B（x₂，0）的抛物线，即判别式Δ=b²-4ac≥0] .

已知抛物线与x轴即y=0有交点A（x₁，0）和 B（x₂，0）,我们可设y=a(x-x₁)(x-x₂),然后把第三点代入x、y中便可求出a。

由一般式变为交点式的步骤：

二次函数

∵由韦达定理得：

x₁+x₂=-b/a；x1·x2=c/a

∴y=ax²+bx+c

=a(x²+b/ax+c/a)

=a(x+b/a)(x-c/a)

令y=0，则解得x₁=-b/a, x₂=c/a. 

重要概念：a，b，c为常数，a≠0，且a决定函数的开口方向。a>0时，开口方向向上；a<0时，开口方向向下。a的绝对值可以决定开口大小。a的绝对值越大开口就越小，a的绝对值越小开口就越大。

其他知识介绍：牛顿插值公式

由此可引导出交点式的系数a=y/(x-x₁)(x-x₂) [y为截距]，二次函数表达式的右边通常为二次三项式。