二元一次方程

二元一次方程其实不难，只要掌握好基本逻辑，就不会被它所“绕晕”。

话不多说，咱们直接列方程。

                

                       

为了方便 “数学学习困难户” 理解，所以例题都是挑最简单、最基础的来讲。

二元一次方程主要有两种解法，一种是代入法，另外一种是消元法。

先说代入法，其中代入法可以选择由y代入x，或由x代入y，这两种形式。

解法1.1

                ①

                       ②

        方程两侧各乘以X。

                

                          ③

        所以 Y 跟 3X 是等价的。

        在方程里可直接把 Y 替换成 3X 。

        在③方程两边各除以 3 ，又可以得到以下的方程。

                ④

        而 X 又与 1/3·Y 是等价的。

        在方程里也可直接把 X 替换成 1/3·Y 。

        Y跟3X是等价的，所以可以把Y-X里的Y替换为3X。③代入①得

                

                         

                            ⑤

            ⑤代入①得

                

                           

                            

我们已经得到了x与y的解，x=11 ，  y=33 。

解法1.2

咱们也可以由⑤代入③，这是解法1.2，为了探索各种解法，让“数学学习困难户”更深入了解解方程的逻辑，所以会讲得比较啰嗦，还请大家多多包涵。

                

                

解法1.3

 1/3·Y跟X是等价的，所以可以把Y-X里的X替换为1/3·Y。④代入①得

                

                        

方程两边各除以2/3。

                        

                            ⑥

        ⑥代入①得

                

                

                            

解法1.4

        ⑥代入④得

                

                            

好了，代入法基本讲全了。接下来我们继续讲消元法。

解法2.1

        ①减③得

                

                      

                                  

                                    

求解y的方法同上，这里就让我偷个懒。

                            

解法2.2

        ①减④得

                

                

                                

                                        

                                            

求解x的方法同上，这里就让我再偷个懒。

平时做题时，可以尝试从多种角度去解题。解方程的方法可以很灵活，不必拘泥于一格。

相信大家在各种解法都可以信手拈来时，也不会被一般的二元一次方程所难倒。

以下，我讲聊一聊非常规的解题方法。

这是我21年7月份某个晚上花了半个小时，才试着用奇怪的方法解出来的。

毕竟我已经有十多年没有做过数学题，解方程的方法，全部都已经还给了老师。

由于 Y/X=3 ,所以我把组成Y除以X等于3的等式都从列了出来。

首先Y代入3，X代入1。得到

                

接着再用3减1。

                

这两个等式归类为一个序列，共列了4组序列。我打算从这4组序列中，找它们的规律来解题。

1、    

                

                

2、

                

                

3、

                

                

4、    

                

                

在此之前，我认为数学应该是依靠计算来得到答案的。

当我从这些等式中推理出答案的时候，觉得自己在作弊。

只要我继续把序列排列下去，那么，我可以直接得到Y-X=22的答案了。

不过我觉得那样已经不仅仅是“作弊”了。所以只列了4组等式。

大家可以试着从这些等式中发现规律。

现在让我给大家理一理我当时的思路。

所有序列的第二个等式，Y除以X，商都是3。

而第一个等式，Y减X，差都是偶数，而且从第一个序列排列到第四个序列。

分别是2、4、6、8……，差都是2的整数倍数。

而且3-1=2、6-2=4、9-3=6、12-4=8，差都是“减数”乘以2的结果。

1×2=2

2×2=4

3×2=6

4×2=8

很好，我已经得到了一个未知数的答案！

Y-X=22，那么用22除以2，商为11。

22加上11，和为33。

接着把33代入Y，11代入X来进行检验。

33-11=22

33÷11=3

跟Y-X=22 , Y/X=3的方程也是相符的。

好吧，虽然我把方程解出来了。而且我尝试把方程的差与商进行更改，再使用这个方法来求未知数，也是可以得到正确的答案。

但是我觉得这是属于旁门左道的作弊行为。反而自己都不好意思认为这样的行为是正确的。

而且大家普遍认为仅仅只是靠找规律来解题，有可能是不靠谱的——只是前几例数字的规律是符合预期，不能保证所有的数字都符合这个规律。

直到前几天，我重新翻看以前的解题过程，才发现……这不是跟一次函数很近似嘛！

实话说出来，也不怕大家笑话。

本学渣直到最近，才开始系统的学习到一次函数。

解出这道题后，又过了一两天，在解其他数学题的过程中，自己渐渐地学会了常规的解方程的方法。

之后，慢慢地不再使用推理的方式去解题，毕竟担心这属于作弊行为，最后连自己都忘了这个方法。

不过，就算我当时继续使用推理的方式去解题，我也不可能把这个方法推广到跟一次函数那样完美。（至少对我来说，一次函数是比较完美的）

因为我在念初中时，对几何课是完全听不懂的。我也不清楚函数图像算不算几何，反正都是画图什么的。

我的推理方法当然没有办法跟一次函数相比，因为这个方法是没有图像的，还是需要进行一些计算，所以没有办法像一次函数那么直观。

而一次函数只需要根据参数画两条直线，相交的点就是答案。

你只需用尺子画横轴和纵轴，确定好两个坐标。

轻松得已经不属于作弊，属于“犯规”了啊！

按一次函数的方法，

Y=X+22

Y=3X

大概是这样的。

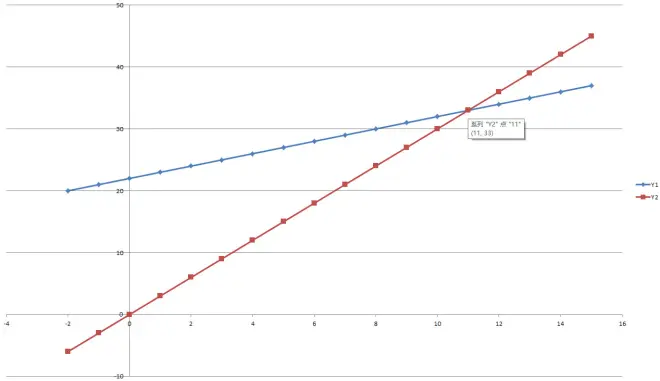
目前我正在学习一次函数中。如果我弄错了，还请大家能够指正。

由于仅靠有限的数据来找规律，很有可能是不靠谱的。所以我想试着来证明这个方法。

                

                        

让咱们来稍微做一些改动，

设已知数3为n(n>1)，a是系数k(k>0)与n-1的乘积。

                ①

                ②

    由②展开得

                ③

    由③代入①

                

                ④

                

    接着让我们整理一下。

                

    所以在这里，X 就是系数 K 。

                 

                     

               

        写证明比想象的更难。受水平所限，我也不知如何写下去了。

        如果觉得对你有帮助的话，还请投币、点赞、关注，一键三连。好了，啰哩巴嗦的写了那么多，今天就忽悠到这里。谢谢大家。