用差分配方法解决一些三元对称不等式

本文要分享的差分配方法是一种可以解决大多数三元对称不等式的方法，不需要什么放缩而是需要一些恒等变形与计算能力，是一种强力且稳定的方法，下面就进行这种特殊配方法的入门指导 小时候，我们曾学过三元均值不等式也就是

如图的证明是常见的，也给我们一定的启发，在证明三元对称不等式的时候，我们是否可以将f（a，b，c）≥g（a，b，c）写成f（a，b，c）-g（a，b，c）≥0，再将左边配成Sa×（b-c）²+Sb×（a-c）²+Sc×（a-b）²的样子呢？事实上很多题目都可以这样做。下面简单句两个例子

可以看到这个题还是比较容易配成我们所说的那种形式，但也给我们配方的方向，首先就是要看取等，因为如果能配成这种形式就必须要有三个相等的取等条件，所以将右边平均分成三份来与左边一一作差，这样就不会破坏对称性。下面来看第二个例子

那么我们就明确了配方的思路 1.要平均分配，不能破坏取等，可以将a，b，c都等于1来带入 2.需要注意不破坏单项的对称性 其次这里奉上一些差分配方法所需要两个的常见恒等式，方便读者牢记

经过这两个简单的例子，我们大致明白了配方的方向，接下来就该挑战一些小有难度的问题了

熟悉此题的同学可能会发现，这道题目的原型不就是3次的舒尔不等式吗？但是舒尔不等式实际上只需要a，b，c＞0就是正确的，那么是不是说明差分配方法的威力不足呢？其实主要是Sa，Sb，Sc都＞0这个条件太苛刻了，因此这里介绍一些定理来带领我们解决更多问题

这三条不等式是显而易见的，于是我们紧接着可以得到下面的定理

所以对于先前的第三道题，在配方完后，设a≥b≥c，就可以得到

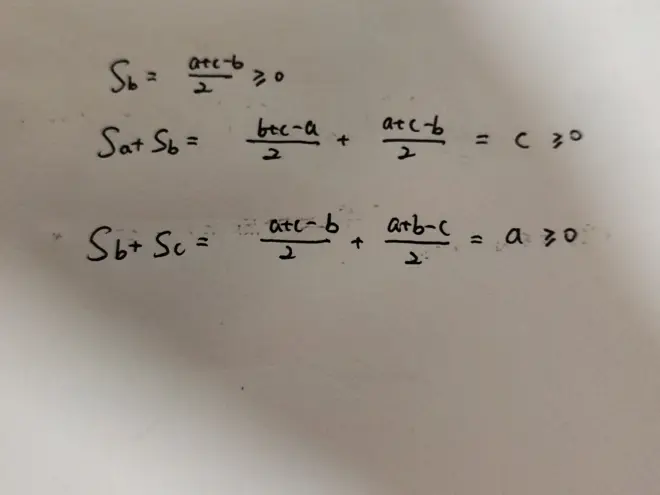
那么由定理①就可以得到a，b，c≥0是，不等式成立，我们就证明了舒尔不等式 总结一下，这种配方法在面对大多数三元对称不等式还是非常好用的，本文只提供了一些简单的问题，事实上差分配方法是可以解决一些很强的不等式的。（主要是看网上都没人发这个方法简单介绍一下）