【官方双语】形象展示傅里叶变换

我们复变与积分变换老师这部分根本不讲，不过考虑到我们是电气专业，更偏向于拉普拉斯变换，这个就当做课外补充。

作者抛出一个物理背景的问题，如何分解复杂叠加波为简单波的线性组合。

选取波的一部分，就把一个图像缠绕在圆上，复杂程度看叠加情况(这可不是简单的缠绕，有点类似与极坐标中摆线：【数学之美-摆线、内摆线、外摆线-数学-物理-Manim-Fun Math, Intelligence Life-哔哩哔哩】 https://b23.tv/dCtGJGI)

像下面这个很快就叠在一起了

或者这种

缠绕是一种变换

这些正弦曲线高低变化他们的叠加并不能简单地线性表示，作者却通过缠绕后的金属丝的圆心的重心的特点找出这些曲线的“浓缩部分”：在这里表现为心形线的偏移重心(见下图说明)

这个是对应拿一半曲线来缠绕叠加的

一半的峰落在右边，一半的峰落在左边，“重心”就落在原点上

接着作者把中心给量化出来，那个心形线的重心非常明显出现一个峰值

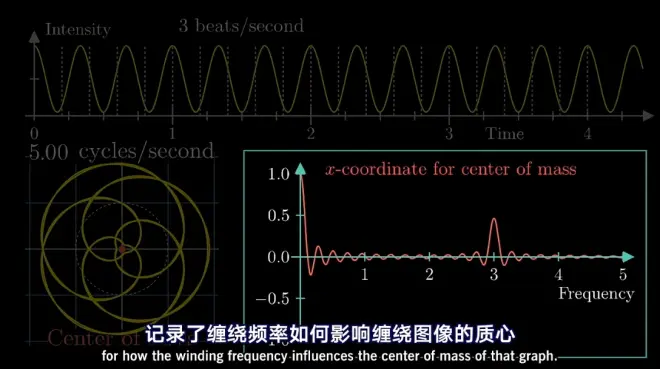
接着作者又证明了，如果竖直位移变化，这个峰值还是没有变化，体现出这个

缠绕的数学表示

这个旋转的复数，依照函数值的大小缠绕。

重心的转换

积分

然后在实际问题我们一般用到无穷，这里上下限给他上一个无穷就变成傅里叶级数了

最后说一点自己的感想：

我个人观点是，如果你想学习好数学，符号推演是必不可少的，图形化只是一个辅助（图形化不能解决具体问题）。

对我而言，我在没有学习系统的高等数学，线性代数，积分变换时看这些视频常常有一种虚假的饱腹感。

但在学过后再看就有一种醍醐灌顶的感觉。特别是一方面目前大学的学科压的很紧，很多数学都不深入，可能到最后记得的东西很少。图形化就可以作为思想上一种粘合剂来加强记忆。另一方面以后理工科很多应用都需要一种直觉来理解为什么要使用这个数学工具，更加方便理解。

有句话叫做：数缺形时少直观,形少数时难入微，我觉得配合食用，效果极佳。