【高等数学第10讲】高阶导数

第十章 高阶导数（侧重计算）

一、知识点

1. 高阶导数定义：
   

   04:32

   
2. 注：f(x)n阶可导=>f(x)直至n-1阶连续可导。
3. 求导与奇偶性的变化：
   

   17:58

   
   （前提：f(x)可导）
4. f(x)奇函数=>f'(x)偶函数（反之不成立）（因为有个C）
5. f(x)偶函数<=>f'(x)奇函数（C不影响函数关于x轴对称）
6. 求高阶导数的方法（显函数）: (归纳法、公式法、泰勒)
   

   28:35

   
7. 归纳法：
   

   29:12

   
8. 直接求，找规律
9. 一些常见函数的n阶导数的记忆：
10. sinx和cosx的n阶导数：
    

    32:11

    
11. (sinx)^(n)=sin(x+n*(π/2))
12. (cosx)^(n)=cos(x+n*(π/2))
13. 幂函数n阶导推论记忆(见图1)：
    

    35:43

    
14. y=ln(1+x)的n阶导数：
    

    39:40

    
15. 转换成求幂函数n-1阶导数问题
16. 两个函数乘积的n阶导（莱布尼兹公式）：
    

    42:14

    
    （见图2）
17. 公式法：
18. 公式见图3
19. 泰勒：
    

    01:01:35

    
    （见图4）
20. 对比：
21. 莱布尼兹公式：两函数乘积的n阶导，n一般取值很大，几十或上百或者就是n
22. 泰勒：两函数乘积有限次较小高阶导
23. 反函数的高阶导数：
    

    01:12:04

    
24. 原函数的一阶导不为0这个条件不能缺少。
25. 求高阶导数的思想跟求反函数的二阶导数一样
26. dx^2与d(x^2)的区别：
    

    01:22:00

    
27. dx^2是微分的幂，d(x^2)是对x^2求微分

图1：

图2：

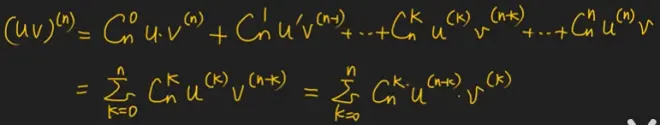
图3：

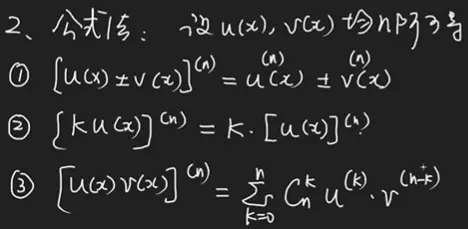
图4：

二、证明

1. 证明“f(x)可导，f(x)奇函数=>f'(x)偶函数，且反之不成立”：
   

   18:60

   

三、计算

1. 考察二阶导数的概念：
   

   10:02

   
2. 利用求导与奇偶性的变化做题：
   

   27:18

   
3. 一眼就能秒，第一次做真的求了三次导。
4. 归纳法+公式法求n阶导：
   

   48:41

   
5. 待定系数拆：
   

   50:46

   
6. 用麦克劳林公式：
   

   01:07:49

   
   （好好体会一下怎么确定拆到哪一项）
7. 第一次看的时候没有搞懂为什么要乘120=>我们求出y的5阶导数系数是8/15，它是由y在0处的5阶导除以5的阶乘得来的。所以y在0处的5阶导=(8/15)*(5!)