为什么连杆可以画出所有曲线

1.什么是连杆系统
(连杆系统)都是由一些刚性的小杆,在端点处,以转轴的方式相连而成。
固定一个连杆系统中某些杆的端点,旋转特定的连杆,系统中其余的动点便可以产生特定的目标轨迹。
最简单的连杆系统:

固定杆OA中的一个端点O,则A的轨迹是一个以O为圆心的圆
一些简单的装置也可以画出极其复杂的图形
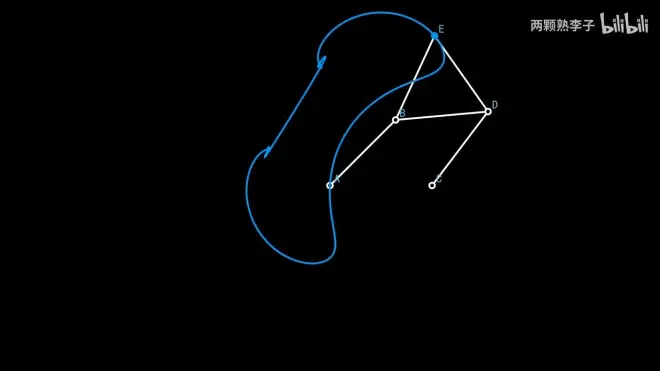
2.如何用连杆系统画直线
帕塞利埃连杆(Peaucellier-Lipkin Linkage)
发明者:Charles Nicolas Peaucellier

AD=AC,BCED为菱形,AO=OB,EG⊥AF
为什么直线?
只需证明AG为定值,便可以说明E在过G垂直于AF的直线上运动
证:∵AD=AC, BD=BC, ED=EC
∴A, B, E三点共线
∵⊙O中AF为直径
∴∠ABF=90°
∵EG⊥AF
∴∠G=90°=∠ABF
∵∠A=∠A
∴△ABF∽△AGE
∴AG/AB = AE/AF
∴AG = AB·AE/AF
#AF为定值,只需证明AB·AE为定值
∵AB=AH-BH, AE=AH+BH
∴AB·AE=AH²-BH²
∵BCED为菱形
∴DC⊥BE
∴AH²=AC²-CH², BH²=BC²-CH²
∴AB·AE=AC²-BC²(之后会用到这个结论)
∵AC, BC为定值
∴AB·AE为定值
∴AG为定值
3.连杆系统几乎万能
连杆系统可以画出所有符合以下要求的代数曲线:

3.1.构造坐标系

OAXB, OCYD为两个全等的筝形,△OAC, △OBD为等腰直角三角形。
这样,Y始终在X关于O逆时针旋转90°的位置上
为什么?
已知:OAXB, OCYD为两个全等的筝形,△OAC, △OBD为等腰直角三角形。
求证:OX⊥OY, OX=OY
证:连接OX, OY

∵OAXB≌OCYD
∴OD=OB, DY=BX, ∠ODY=∠OBX
∴△ODY≌△OBX(SAS)
∴∠1=∠2, OX=OY
∵△DOB为直角三角形
∴∠DOB=90°
∴∠XOY=∠DOB-∠1+∠2=90°
—— —— —— —— ——
把X连接在Peaucellier连杆上,X, Y就会分别在两条相垂直的直线上运动

之后会省略Peaucellier连杆。
3.2.如何画出任意曲线
我们将OX, OY的长度定义为自变量 t

为画出任意曲线,连杆需要且只需要实现4条功能:
1、把某个点的坐标加上一个常数c;
2、把某个点的坐标乘上一个常数c;
3、把两个点的坐标相加;
4、把两个点的坐标相乘。
为了实现这些功能,我们设计了以下7个装置:
3.2.1.常量加法器

固定一段连杆(AB为定值),用两个平行四边形(橙色)把固定长度(AB)传递到坐标轴上(XD)
两个被加数:OX、AB
和:OD
常量加法器支持矢量运算。
3.2.2.固定器

利用三角形的稳定性,使杆与杆(图中为蓝杆和绿杆)之间的位置关系保持不变
3.2.3.常量乘法器

由两个固定器组成
AP=BC, AB=CP
∴ABCP为平行四边形
∴AP//BZ, CP//OB
∴△OAP∽△OBZ
—— —— —— —— ——
两个被乘数:AP、OB/OA
积:OZ
常量乘法器支持矢量运算
3.2.4.加法器

加法器非常重要,它不仅要加减法,还要将X, Y轴的坐标算成最终的结果
四个小四边形都是平行四边形,
所以OAFB也是平行四边形

证:连接OA, AF, FB, BO
∵▱ADEH
∴AH//DE, AH=DE
同理DE//OC
∴AH//OC, AH=OC
同理FH//BC, FH=BC
#下一行中我少写了很多步骤
∴∠AHF=∠OCB
∴△AHF≌OCB(SAS)
∴AF=OB
同理AO=BF
∴AOBF为平行四边形
—— —— —— —— ——
两个被加数:向量OA、向量OB
和:向量OF
3.2.5.减法器

减法器也是一个加法器,但比较特殊。
两个被加数:向量BO、向量BA
和:向量BF
3.2.6.倒数器

DAEB为菱形,OA²-AD²=1
这时候,我们需要用到我们之前在Peaucellier连杆中的结论。

我们曾经说到AB·AE=AC²-BC²,所以在这里,我们只需要确认OA²-AD²=1,就可保证OD·OB=1
OD、OB互为倒数
3.2.7.乘法器
乘法公式:p·q=((p+q)² - (p-q)²) /4
所以要乘法,我们要学会平方
我们知道:1/(p-1) - 1/(p+1) = 2/(p²-1)
变换得:p² = 2 / (1 /(p-1) - 1 /(p+1)) +1
所以我们只需要用在倒数器基础上,再进行一堆操作,就可以实现乘法了。
具体过程作者懒得说,那我就更懒得说了(
最后不能展示乘法器,因为渲染不完
—— —— —— —— ——
把上述的7个装置巧妙地结合起来,就几乎可以画出任何图像了。
end
—— —— —— —— ——
后记:这应该是我写得最久的一次笔记了,好累……

