【WSN】异构无线传感器网络的开发分布式节能集群算法(DDEEC)附matlab代码
✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab完整代码及仿真定制内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器 电力系统
信号处理 图像处理 路径规划 元胞自动机 无人机
🔥 内容介绍
无线传感器网络(Wireless Sensor Network,简称WSN)是一种由大量分布式传感器节点组成的网络,用于监测和收集环境中的信息。WSN的应用范围广泛,包括环境监测、农业、医疗、交通等领域。然而,WSN面临着能源有限、节点功耗不平衡等问题,这些问题严重影响了网络的性能和寿命。
为了解决WSN中的能源问题,研究人员提出了各种能源节约的算法和协议。其中,分布式节能集群算法(Distributed Energy-Efficient Clustering,简称DDEEC)是一种常用的算法。DDEEC算法通过将网络节点划分为多个集群,每个集群由一个簿记节点(Cluster Head)负责管理和协调。簿记节点负责收集并汇总集群内其他节点的数据,并将数据传输到基站。
DDEEC算法的核心思想是通过选择合适的簿记节点来减少网络中节点的能量消耗。在算法的初始阶段,每个节点都有机会成为簿记节点。节点根据其剩余能量和与基站的距离来计算能量消耗指标,选择能量消耗最小的节点作为簿记节点。选定簿记节点后,其他节点将加入到与其距离最近的簿记节点所在的集群中。
为了进一步减少能量消耗,DDEEC算法引入了轮流工作的概念。每个集群中的节点将根据轮流工作的规则,在不同时间段内交替充当簿记节点和普通节点。这样可以平衡网络中节点的能量消耗,延长整个网络的寿命。
DDEEC算法在实际应用中取得了良好的效果。通过合理地选择簿记节点,能够减少节点之间的通信开销,提高网络的能量利用率。同时,通过轮流工作的机制,能够避免节点能量消耗不均衡的问题,延长整个网络的寿命。
然而,DDEEC算法也存在一些挑战和限制。首先,算法需要节点之间进行频繁的通信,增加了网络的能量消耗。其次,算法在网络规模较大时,簿记节点的选择可能会变得复杂和困难。此外,算法对网络拓扑结构的依赖较强,不适用于某些特殊环境下的应用。
为了进一步提高WSN的能源利用效率,研究人员需要继续改进和优化DDEEC算法,解决其存在的问题和限制。同时,还需要开展更多的实验和仿真研究,验证算法的性能和可行性。
总之,DDEEC算法是一种有效的分布式节能集群算法,可以在异构无线传感器网络中减少节点的能量消耗,延长网络的寿命。然而,该算法仍然存在一些挑战和限制,需要进一步的研究和改进。通过持续的努力,相信可以开发出更加高效和可靠的节能算法,推动WSN技术的发展和应用。
📣 部分代码
clear allxm=100;ym=100;sink.x=0.5*xm; %location of sink on x-axissink.y=0.5*ym; %location of sink on y-axisn=100 %nodesP=0.1; %probability of cluster headsEo=0.5;%initial energy%Echeck=Eo;%ETX=50*0.000000001; %tx energyERX=50*0.000000001; %rx energyEfs=10*0.000000000001; %free space lossEmp=0.0013*0.000000000001; %multipath loss%Data Aggregation EnergyEDA=5*0.000000001; %compression energya=1; %fraction of energy enhancment of advance nodesrmax=5000 %maximum number of roundsdo=sqrt(Efs/Emp); %distance do is measuredEt=0; %variable just use below m=0;mony=0;c=0.02;b=0.7;talhar=0;for i=1:1:n S(i).xd=rand(1,1)*xm; %generates a random no. use to randomly distibutes nodes on x axis XR(i)=S(i).xd; S(i).yd=rand(1,1)*ym; %generates a random no. use to randomly distibutes nodes on y axis YR(i)=S(i).yd; S(i).G=0; %node is elegible to become cluster head talhar=rand*a S(i).E=Eo*(1+talhar); S(i).A=talhar; E(i)= S(i).E; if (E(i)>Echeck) mony=mony+1; end Et=Et+E(i); %estimating total energy of the network %initially there are no cluster heads only nodes S(i).type='N';endm=mony/100;d1=0.765*xm/2; %distance between cluster head and base stationK=sqrt(0.5*n*do/pi)*xm/d1^2; %optimal no. of cluster headsd2=xm/sqrt(2*pi*K); %distance between cluster members and cluster headEr=4000*(2*n*ETX+n*EDA+K*Emp*d1^4+n*Efs*d2^2); %energy desipated in a roundS(n+1).xd=sink.x; %sink is a n+1 node, x-axis postion of a nodeS(n+1).yd=sink.y; %sink is a n+1 node, y-axis postion of a nodecountCHs=0; %variable, counts the cluster headcluster=1; %cluster is initialized as 1flag_first_dead=0; %flag tells the first node deadflag_teenth_dead=0; %flag tells the 10th node deadflag_all_dead=0; %flag tells all nodes dead
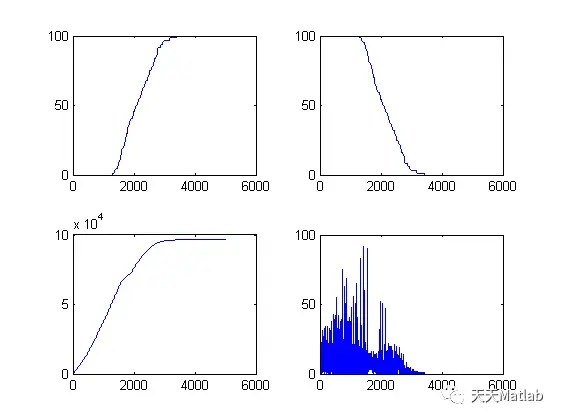
⛳️ 运行结果