11:4 他们说、来吧、我们要建造一座城、和一座塔、塔顶通天、为要传扬我们的名、免得我们分散在全地上。

11.4 Tembis, ”Spana! Kemola kation mo tupen amantte faletesa nomen dix fiatate din solialete joven.”

——《圣经·创世记》

观前提示：

为了更好地保证阅读体验，希望读者能够具有一定的语言学知识。（实在没有也不用过于担心，会有一定的讲解的）

笔者由于自身知识限制，难免会出现一些错误。如果有读者发现错误，可以直接私信笔者，笔者将不胜感激。

笔者因为学习工作原因，更新时间和回复私信时间均不固定，还请谅解。

为什么突然又更回第一章了？

这主要是因为在语言创造的过程中出现一些新的现象，而原来的语法介绍并不能全面地归纳总结。还有一种情况是旧有的语法发生了冲突，需要进行修改、删减和补充。这种补充类介绍以后还会出现。

目前预定的补充篇划归章节的原则是：如果谈论内容集中于某一个部分，比如集中讨论名词，则划归到和其内容对应的章节；如果内容较多较杂，就明确表示“补充”“杂”等字样，或用X来代替章节名。

第一点五变格法？

这个标题当然是调侃，但它确实反映了一部分名词的变格特点，即单数变格参照第一类复数变格，双、复数变格参考第二类对应的名词（实际上双数极少用到）。例如：

spanatus n.到来（）

（格 单数 双数 复数）

nom: spanatus spanatusir spanatusis

acc: spanatuen spanatusiren spanatusin

gen: spanatux spanatusirex spanatusix

...

/*

nom: nominative case 主格

acc: accusative case 宾格

gen: genitive case 属格

*/

可以看到，按照之前的变格法，spanatus应该属于第二变格法（以-s/t结尾），其单数变格应该为spanatus(nom.), spanatusen(acc.), spanatusex(gen.), …但这里的单数变格却形如第一变格法的复数变格。详情查看【人造语言】曼都语 1.2.1 名词的格及其用法（1）。而双数和复数变格却遵照第二变格法，这在曼都语中被称为杂合名词（sonna kimeral），通常包括一下几种情况：

1）所有动词的动名词形式。比如上面的示例spanatus就是spanate (vt. 来) 的动名词形式，属于此类。除此之外的例子还有antitus(到来), venitus(拜访), prifetus(起义) 等。至于动名词的内容会在后面动词的非谓语用法中给出。

2）一些名词的复数形式衍生出的名词。比如曼都：Mandus，就是mando（领土）的复数主格形式衍生而来。

3）由上述两类名词再次衍生的，单数主格形式形同第二变格法名词的名词。如alderus(词缀)由alderite（装饰、点缀）的动名词形式alderitus派生而来。

不难发现，以上的例词都以-us结尾。事实上，绝大多数杂合名词都以-us结尾，极少数以-es结尾（屈指可数）。因此杂合名词有时又被称为-us类名词。

双数的双数、双数的复数、复数的双数、复数的复数——对第二变格法的延拓

先来看这样一个例子：

kuibieso n.夫/妻

这个词和英文中的parent很类似，都是表示双方中的任意一方。我们知道，曼都语的双数通常表达成对的东西，因此下面两种表达方式就有不同的含义：

（双数）kuibiesur 夫妻

（复数）be kuibiesus 两个有家室的人

然而，对于表达“多对夫妻”，就会出现表达歧义，因为复数不考虑成对与否，简单根据数量的话，很容易翻译为“kuibiesus”，按照前面的例子，有极大的可能会被理解为“多个有家室的人”（大家可以想一想这种场景，是不是有多人运动那味了）。所以为了避免这种歧义，我们对曼都语的第二变格法进行延拓，也就有了针对本节标题中的四种情况展开的对名词变格法特殊用法的讨论。

第二变格法是基于名词以-s/t结尾的情况成立的。但，如果我们再查看一遍变格表……

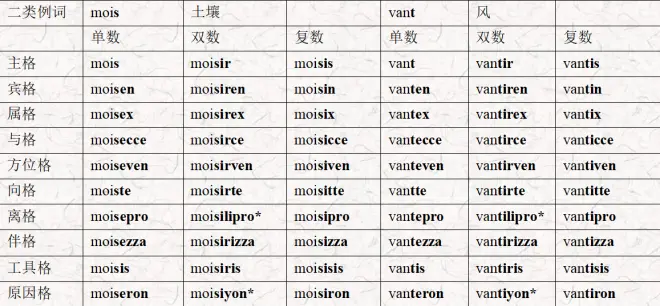
我们会发现，这里的变格是纯粹的黏着，既不像第一、四变格法中o -> u, a -> e, e ->i的变元音，也没有第三变格法中n -> nn的辅音变化。因此，这意味着第二变格法的实际适用情况可以拓展到一切以非n辅音结尾的单词，只不过由于历史原因，字典中收录的以辅音结尾的单词全部演变为以-s/t结尾（不要问外来语是怎么回事，问就是第四变格法是个口袋变格法，哪里需要往哪搬[doge]）。

有了这个认识，上面的问题就好解决了。再重新请出我们的kuibieso。先变为双数主格形式kuibiesur，再以kuibiesur为“第二类名词”进行主格复数变化为kuibiesuris，这样就可以表示“多对夫妻”了。

现在返回来看杂合名词，其实也能用第二变格法的延拓解释，因为在曼都人的观念中，无论是动名词还是集合名词，理论上都是复数的。对于这些在理论上是复数，实际中却被当作“单个整体”使用的名词，自然也需要通过第二变格法的延拓来完成所谓“双数的复数”“复数的复数”之类的情况。我们来看这样一个例子：

Yo be Mandusis! 没有两个曼都！

这里的Mandusis就是Mandus的复数，也可以看作mando的复数形式的复数。不过鉴于其本身是一个专有名词，自然也可以直接将Mandus看作一般的第二类名词。

既然有了双数的双数、双数的复数、复数的双数、复数的复数，这也意味着名词还可以在这四种基础上再进行延拓变格，最终达到多层套娃的效果。（话说真的有人会用吗）

需要注意的是，这种变格的原则和其他变格法一样，都是先变数，后变格！一旦进行格的变化，那么就数的变化也就终止了。

名词的名词化

你可能看了觉得很奇怪：为什么名词还能名词化？

除了主、宾格外，其他第一类格形式的名词都不能作为主、宾语。但这些名词可以经过通过黏着一定的后缀来重新构成具有特殊意义的名词来担任主、宾语。在这些词后加-etta构成，表示“......的”，具体指代什么，若无上下文指明，则泛指人、事、物。这些名词被归入第一类名词。如：

——N’esus spano feveran sa? 那些人来是为了花吗？

——Feveronettes spanon s’akötte.找花的（人）不会来这。

(feva--feveron--feveronetta--feveronettes，为了花的人们)

不过这是相对早期的语法，现代曼都语中这样的用法已经不多见了。

预告

上一篇专栏就动词的变位结构和其第一步——基本形进行了介绍，下一篇开始将对其第二部分，也就是动词的极性进行介绍。如果篇幅有余裕，还会介绍动词的语态和语气。这里是滕达·艾勒·阿卡叙加斯，我们下个专栏再见。

——To be continued