【中算】勾股定理:“双矩重迭图”
郑涛(Tao Steven Zheng)著
据三国时代数学家赵爽《周髀算经注》:
两差相乘倍而开之, 所得以股弦差增之为勾。以勾弦差增之为股。两差增之为弦。
今译:两差(“勾弦差”和“股弦差”)相乘,加倍,开方,所得加上股弦差,等于勾;所得加上勾弦差,等于股;所得加上两差,等于弦。
在这段文中,赵爽指出关于勾股形(直角三角形)其中一个恒等式以及应用。
两差相乘倍而开之:
所得以股弦差增之为勾:
以勾弦差增之为股:
两差增之为弦:
这些公式是从哪里来的?中国古代数学家习惯用图来解析几何公式。用于推导以上公式的图叫作“勾股双矩重迭图” 。
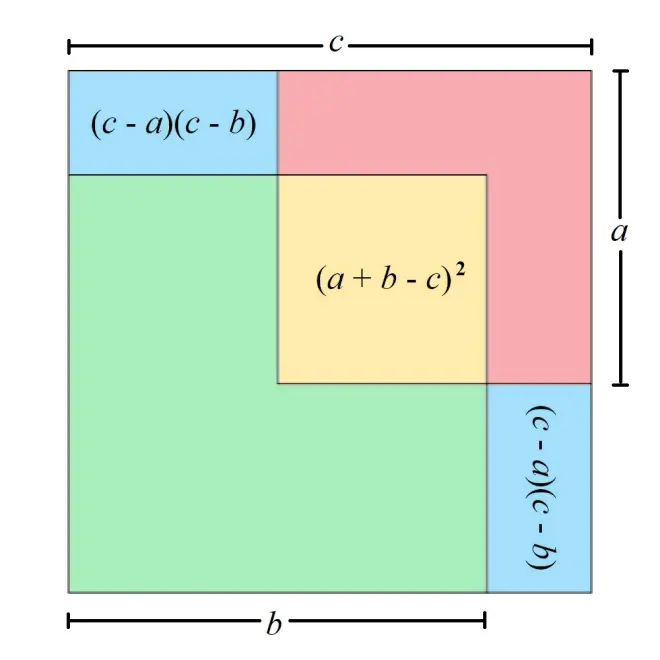
根据 “勾股双矩重迭图”,勾方的面积为 ,股方的面积为
,弦方的面积为
;黄方部分为勾方和股方相重迭的正方形,其面积为
;相对的两个青矩形的面积都是
。由图可见
根据勾股定理 ,得
开方即得
《九章算术》第九卷 “勾股” 第十二题也有使用这些公式。
今有户不知高、广,竿不知长短。横之不出四尺,从之不出二尺,邪之适出。问:户高、广、袤各几何?
今译:假设有一门户,不知道它的高和广,有一根竹竿,不知道它的长短。将竹竿横着,有4尺出不去,竖起来有2尺出不去,将它斜着恰好能出门。问:门户的高、广、斜各是多少?
这道题的 “横之不出” 和 “从之不出” 就是 “勾弦差” 与 “股弦差”。
题解在这里:
【中文版】https://www.bilibili.com/read/cv13299296
【英文版】https://www.bilibili.com/read/cv13298996

