python使用matplotlib绘制简单图形

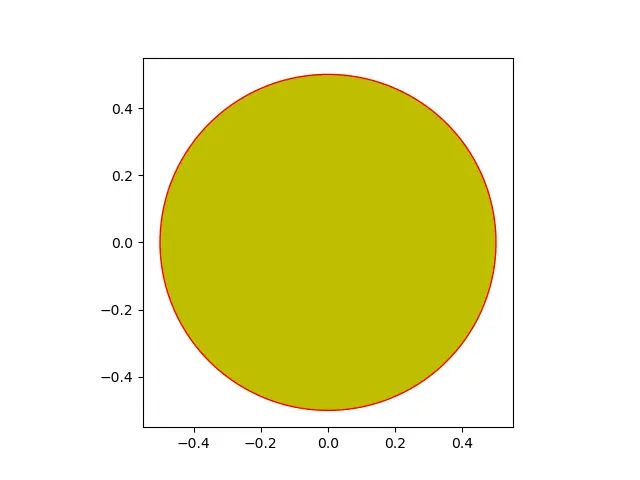
1，绘制一个圆

import matplotlib.pyplot as plt

def creat_circle():

    circle=plt.Circle((0,0),radius=0.5,fc='y',ec='r')#圆心坐标，半径，内部及边缘填充颜色

    return circle

def show_shape(path):

    ax=plt.gca() #获取当前对象

    ax.add_patch(path) #给对象传递添加的块

    ax.set_aspect('equal') #设置图形的宽高比，equal为1:1

    plt.axis('scaled') #设置自动调节数轴范围

    plt.show()

c=creat_circle()

show_shape(c)

2，绘制动图

from matplotlib import pyplot as plt

from matplotlib import animation

def creat_circle():

    circle=plt.Circle((0,0),radius=0.05,fc='y',ec='r')#圆心坐标，半径，内部及边缘填充颜色

    return circle

def update_radius(i,circle):#调用时自动传递的帧编号，每一帧需要的对象；返回也是一个帧对象

    circle.radius=i*0.5

    return circle

def creat_animation():

    fig=plt.gcf() #获取当前Figure对象的引用

    ax=plt.axes()#创建坐标系并设定取值范围

    plt.xlim(-10,10),plt.ylim(-10,10)

    ax.set_aspect('equal')

    circle=creat_circle()

    ax.add_patch(circle) #将圆添加到当前坐标系下

    anim=animation.FuncAnimation(

        fig,update_radius,fargs=(circle,),frames=30,interval=50)#传给FunAnimatin绘制动图的参数

    #依次为:当前Figure对象,绘制每帧的函数,给前面的函数通过元组传递参数(帧数不用传递)

    #帧数(这里选30帧),两帧之间的时间间隔(这里是50毫秒)

   

    plt.title('Dynamic circle')#设置标题

    plt.show() #显示动图

    anim.save('circle.gif',writer='imagemagick')#在当前目录下保存动图

creat_animation()

3，绘制抛物线动图：

from matplotlib import pyplot as plt

from matplotlib import animation

import math

g=9.8

def get_intervals(u,theta): #u为初合速度，theta为合速度与地面夹角

    t_flight=2*u*math.sin(theta)/g

    #由抛物线公式得：总飞行时间为两倍的竖直方向速度除竖直加速度g

    intervals=[]

    start=0

    interval=0.005

    #以0.5为间隔创建列表，以便于后续帧与帧之间代表物体运动的时间间隔为0.5

    while start<t_flight:

        intervals.append(start)

        start+=interval

    return intervals

def update_position(i,circle,intervals,u,theta):#更新每一帧坐标

    t=intervals[i] #传递每一帧对应的物体实际运动时间

    x=u*math.cos(theta)*t

    y=u*math.sin(theta)*t-0.5*g*t*t

    #根据抛物线公式算出确定时间下对应的位置坐标

    circle.center=x,y #传入球心坐标

    return circle

def create_animation(u,theta):

    intervals=get_intervals(u,theta)

    xmin,ymin=0,0

    xmax=u*math.cos(theta)*intervals[-1]

    #以最大时间值算出x坐标最大值

    tmax=u*math.sin(theta)/g

    #飞到最高点所用时间

    ymax=u*math.sin(theta)*tmax-0.5*g*tmax**2

    #最高点纵坐标

    fig=plt.gcf()

    ax=plt.axes()

    plt.xlim(xmin,xmax),plt.ylim(ymin,ymax)

    circle=plt.Circle((xmin,ymin),0.1) #从起点开始画圆

    ax.add_patch(circle)#添加圆在坐标系下

    ax.set_aspect('equal')

    anim=animation.FuncAnimation(fig,update_position,fargs=\

    (circle,intervals,u,theta),frames=len(intervals),interval=1)

    #这里可以参加参数repeat=False让动图不要无限重复

    plt.title('parabolic movement')

    plt.xlabel('X')

    plt.ylabel('Y')

    plt.show()

    anim.save('move.gif',writer='imagemagick')

try:

    u=float(input('enter the initial velocity:'))

    theta=float(input('enter the angle of projection:'))

except: #避免错误输入

    print('wrong input')

else:

    theta=math.radians(theta)#转为弧度制

    create_animation(u,theta)

当我输入初速度为10，角度为45

4，绘制分形：

'''

绘制分形:

其实就是由一些简单的图形组合而成

这些独立的图形需要提供初始位置和递推关系式(类似于数列的感觉)

下面举一个随机游走的例子，即下一个点的坐标，横坐标加一，纵坐标可能加一或者减一

'''  

from matplotlib import pyplot as plt

import random

def trans1(p):#p为储存x,y坐标的元组，先往下看

    #纵坐标+1

    x=p[0]

    y=p[1]

    return x+1,y+1

def trans2(p):

    #纵坐标-1

    x=p[0]

    y=p[1]

    return x+1,y-1

def transform(p):

    trans=[trans1,trans2] #将函数作为对象

    t=random.choice(trans) #随机选择一个函数

    x,y=t(p) #对选中的函数进行调用

    return x,y

def update_site(p,n):#n为坐标随机更新次数

    x=[p[0]]

    y=[p[1]]#创建列表先存入初始坐标

    for _ in range(n):

        p=transform(p) #随机调用函数更新坐标

        x.append(p[0])

        y.append(p[1])#存入更新后的坐标值

    return x,y #返回完整的坐标列表

p=(1,1) #初始位置

n=int(input('enter the number of tries:'))

x,y=update_site(p,n)

plt.plot(x,y) #根据返回列表绘制

plt.xlabel('X')

plt.ylabel('Y')

plt.show()

比如我输入10000

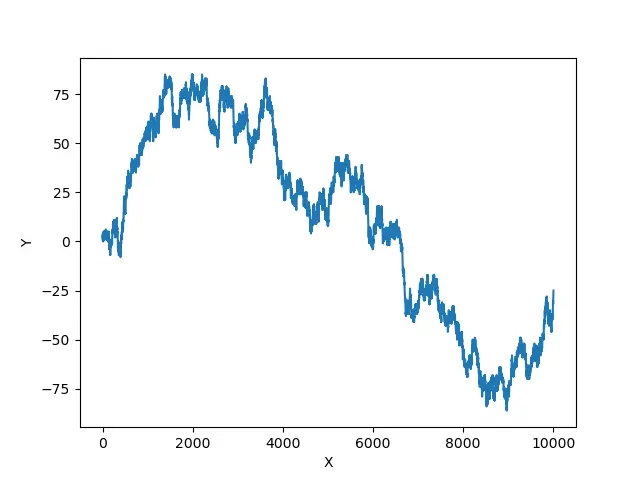
同样的输入，每次输出结果也不一样。

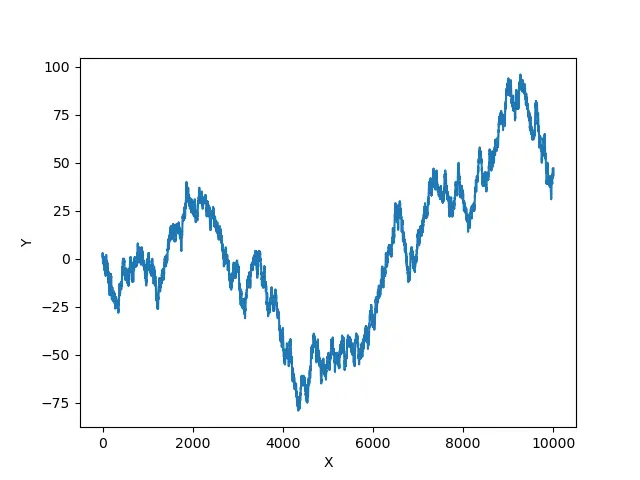
5，更有趣的是，我们可以绘制一些有趣的图形。

原理：以一个确定的点，但按照实现分配的概率执行变换规则（依概率执行递推关系式）

from matplotlib import pyplot as plt

import random

def trans1(p):

    x=p[0]

    y=p[1]

    x1=0.85*x+0.04*y

    y1=-0.04*x+0.85*y+1.6

    return x1,y1

def trans2(p):

    x=p[0]

    y=p[1]

    x1=0.2*x-0.26*y

    y1=0.23*x+0.22*y+1.6

    return x1,y1

def trans3(p):

    x=p[0]

    y=p[1]

    x1=-0.15*x+0.28*y

    y1=0.26*x+0.24*y+0.44

    return x1,y1

def trans4(p):

    x=p[0]

    y=p[1]

    x1=0

    y1=0.16*y

    return x1,y1

#非均匀随机数

def unequal_probability_random_number(probability):

    #输出调用函数的位置

    begin=0

    sum_probability=[] #从分布函数角度来实现

    for p in probability:

        begin+=p

        sum_probability.append(begin) #记录每个离散点的分布函数值

    r=random.random() #产生0到1均匀随机数

    for index,distribution in enumerate(sum_probability):

        if r<=distribution:

            return index

    return len(probability-1)

def transform(p):

    trans=[trans1,trans2,trans3,trans4]

    probability=[0.85,0.07,0.07,0.01]#设置各个函数调用概率

    site=unequal_probability_random_number(probability)

    t=trans[site] #依概率选择一个函数

    x,y=t(p) #对选中的函数进行调用

    return x,y

def update_site(n):

    x=[0]

    y=[0]#创建列表先存入初始坐标

    x1,y1=0,0

    for _ in range(n):

        x1,y1=transform((x1,y1))

        x.append(x1)

        y.append(y1)#存入更新后的坐标值

    return x,y #返回完整的坐标列表

n=int(input('enter the number of tries:'))

x,y=update_site(n)

plt.plot(x,y,'o') #绘制点

plt.xlabel('X')

plt.ylabel('Y')

plt.show()

比如输入n=1000

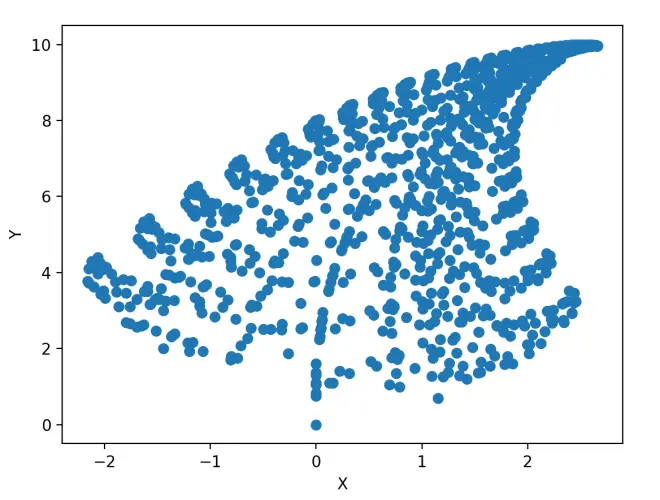
亦或者输入n=5000

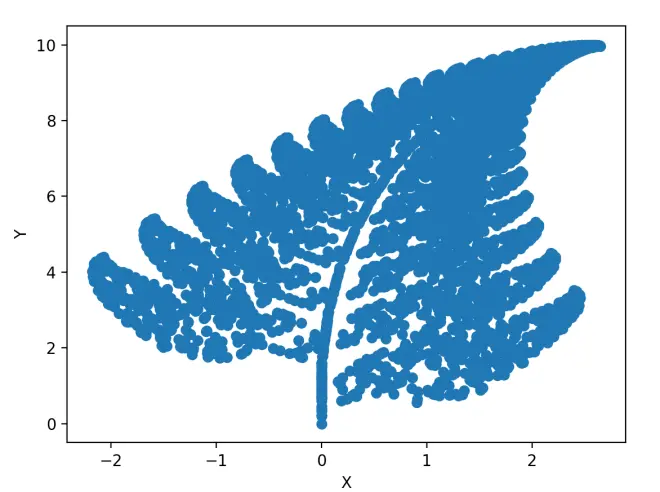
恩，它现在很像一个蕨类植物了，有趣吧~~~