Unit8(8.1-8.4)多元函数微分
Unit8(8.1-8.4) 多元函数微分
一、导言:
在学完了空间坐标系之后,我们的目光从二维的平面投向三维的空间,点不再仅仅存在于一个平面上,而是存在于立体的空间之中。而一组点,也就是点集,为了方便探讨它们之间的内在联系,我们用多元的方程来描述点。
在之前,点的领域包括数轴正负两个方向。趋近某点时,只会有左趋近和右趋近两种方式,而放在平面中,点的领域呈现圆形,有不同种方式趋近它。平面上,由点构成的点集与点形成关系,分为内点,边界点,外点,聚点,孤立点。而又根据点集本身性质,分为开集,闭集,连通集,以及有界集与无界集。这些关系都将在正文细说。
在研究完点之后,我们将目光投向多元函数。多元函数,顾名思义就是一个函数里不再只有一个变量,而是有多个变量,而且通常情况下,这些变量之间是没有联动关系的,说白了就是各变各的,x动不影响y也动。主要知识点包含了多元函数的极限,连续,偏导,微分(全微分,偏微分),其实都是从一元函数中汲取理论来研究多元函数。
二、正文
Ⅰ点集(在二维平面上的):E={(x,y)}|(x,y)满足条件T}
1.点集领域
(1)领域: U(P0,δ),表示P点,|PP0|<δ,
即[(x-x0)^2+(y-y0)^2]^0.5<δ
(2)去心领域:U*o(这里特指去心领域)(P0,δ),表示P点,0<|PP0|<δ,
即0<[(x-x0)^2+(y-y0)^2]^0.5<δ,不包含P0点
2.点集
(1)关系
①内点:ョU(P),st U(P)⊂E。 简单理解,就是一片区域的点中,点在这片区域的内部

②外点:ョU(P),st U(P)∩E=Ø。 简单理解,就是一片区域的点中,点在这片区域的外部

③边界点:∀U(P),st此领域既有E中的点,也有E外的点,记为∂E

④聚点:∀δ>0,st U*o(P,δ)∩E≠Ø。简单理解,就是包括所有内点,以及不作为孤立点的边界点)

⑤孤立点:ョδ>0,st U(P)∩E={P},简单理解就是一片点外孤立一个点,呈现飞岛状,就是这种点是边界点,但不是聚点。

(2)集
①开集:由内点构成开集
②闭集:闭集=开集+边界
③连通集:点集任意两点,可以用包含于E的折线(即线的所有点都在E内)连接。
④连通的开集:(开)区域;连通的开集+边界=闭区域
(3)有界集与无界集:
ョδ>0,st E⊂U(0,δ),则E有界,且其直径为D=max{|P1P2|},若不存在,则称E无界。通俗理解,就是以原点为圆心,画一个圆,如果有一个圆可以包含点集,那么就是有界的,如果找不到这种圆,就是不存在的
Ⅱ多元函数及其性质
1概念
(1)多元函数定义(这里主讲二元函数):z=f(x,y),(x,y)∈D
也可写作z=f(P),P∈D
那么f(D)表示z值整体,即值域,f(D)={z|z=f(x,y),(x,y)∈D}
(2)性质:多元函数的性质与一元函数类似,比如有界无界性质,以及闭区间的最值定理,介值定理,与一元函数相似,不赘述了。
2极限:多元函数的极限是重中之重,在后面定义法求导数里有着极为重要的运用,求法也不像一元函数极限一样手段单一。
(1)定义(并不重要,大概不会出题考)
Z=f(x,y),D⊂R^2(就是坐标平面),P0(x0,y0)为D的聚点,
ョA,∀ε>0,ョδ>0,使得P(x,y)∈【U*o(P0,δ)∩D】时,有
|f(x,y)-A|<ε
则:lim f(x,y)=A
x→0
y→0
其它写法:
①Lim(P→P0)f(P)=A
②Lim f(x,y)=A
(x,y)→(x0,y0)
③Lim f(x,y)=A
|PP0|→0
(2)两种题型:求极限与证明极限不存在
①存在:如果极限存在,那么说明无论任何方向趋近该点,极限值都是相等的。而且若下述三者均存在,则三者相等,Lim f(x,y)|(x,y)→(x0,y0)
=lim(x→x0)【lim(y→y0)f】
=lim(y→y0)【lim(x→x0)f】
求极限有很多种手段,
有x,y整体换元法:

令t=xy,x,y趋于0时t也趋于0
原式=lim(t→0)【2-(t-4)^0.5】/t
用洛必达法则,求得结果为-1/4
有均值不等式放缩,利用夹逼准则,凑有界乘以无穷小:

根据均值不等式:x^2+y^2>=2xy
原式=x xy/(x^2+y^2)
|xy/(x^2+y^2)|<0.5,为有界量, x趋于0
所以原式=0
也有最常见的定一求一法:


②不存在:以不同路径趋于P时极限值不一样或者有不存在的情况。解决证明极限不存在的题目的核心要义就是“搞破坏”,就是找到两条路径,使得极限值不一样,只要找到两个不一样就是不存在。
例证:

①令x=ky
②原式=lim(x→0)(y→0)(ky2+y2)/k2y2+y2= (k+1)/k2+1
③当k取值不同时,极限值不唯一,故不存在
3.连续
(1)定义(函数值等于极限值,以及x,y趋于0时z变化为0)
①lim f(P0)=f(x0,y0)
|PP0|→0
②lim Δz=0
Δx→0,Δy→0
(2)连续函数:一元,二元的基本初等函数以及其有限四则运算,复合运算的函数连续
(3)间断点,间断线:多元函数的间断点很容易组成间断线,本质是定义域的取舍。
4.偏导
(1)概念:定义法求偏导:(以对x偏导为例)
Lim 【 f(x0+Δx,y0)-f(x0,y0)】/Δx
Δx→0
=∂z/∂x |x=x0,y=y0
=Zx(x0,y0)
(2)几何意义:fx(x0,y0)为P0处切线对x轴的斜率。当然了,对什么字母偏导就是对此轴的斜率
(3)高阶:
∂/∂x(∂z/∂y)=∂^2 z/(∂y ∂x)=f yx(x,y)(先对y求偏导,再对x求偏导。本质就是先把y看成唯一的自变量,x看为参数,后面在把y看成参数,
X看成自变量的过程,本质就是多元函数的一元研究方式)
重点:如果f yx(x,y),f xy(x,y)在D区间内连续,那么两者就相等。
5.微分
(1)偏增与全增
①偏增(以x为例子)ΔZx=f(x0+Δx,y0)-f(x0,y0)
②全增:ΔZ=f(x0+Δx,y0+Δy)-f(x0,y0)
③可微:如果Δz可以表示为:AΔx+BΔy+o(ρ),ρ=[Δx^2+Δy^2]^0.5
那么则称此点可微。你看这个地方,还是Δz可以表示为Δx,Δy的线性形式,在趋于0时得到化曲为直的效果,那么既然在趋近0时可以线性表示,此点便是可微的。如果D内各点都是可微的,那么D区间就是可微区间。
(2)可微必然导致连续,而如果z=f(x,y)在U(P0)内有连续偏导,则P0处可微.下面要证明全微分公式:dz=∂z/∂x dx+∂z/∂y dy 。这个公式细化了A,B的具体指代。
①全增转偏增:
Δz|P0=
【f(x0+Δx,y0+Δy)-f(x0+Δx,y0)】+【f(x0+Δx,y0)-f(x0,y0)】
②拉格朗日中值:
f(x0+Δx,y0+Δy)-f(x0+Δx,y0)=f(x0+Δx,θΔy+y0)Δy
θ1在0到1之间
同理f(x0+Δx,y0)-f(x0,y0)= f(x0+θ2Δx,y0)Δx
③P0(x0,y0)连续
Lim fy(x0+Δx,θΔy+y0)=fy(x0,y0)
Δx→0,Δy→0
④类似于泰勒展开时的佩亚诺余项
f(x0+Δx,θΔy+y0)= fy(x0,y0)+α
α=o(ρ)
同理f(x0+θ2Δx,y0)=fx(x0,y0)+β
β也为ρ的高阶无穷小
⑤Δz|P0=
fy(x0,y0)Δy+αΔy+ fx(x0,y0)Δx+βΔx
⑥根据定义,如果Δz可以表示为:AΔx+BΔy+o(ρ),ρ=[Δx^2+Δy^2]^0.5 ,那么则称此点可微。
只需要证明αΔy+βΔx为ρ的高阶无穷小即可(两个和分别除以ρ即可得证)
⑦Δx→0,Δy→0时,Δy=dy,Δx=dx,fy(x0,y0)= ∂z/ ∂y|P0
fx(x0,y0)= ∂z/ ∂x|P0
6.求导:
(1)归一求导:z=f(u,v),u=u(t),v=v(t),那么此时z其实本质就是一个关于t的一元函数,化多为一方便求导。证明下述公式很简单:就是在全微分的基础上整体除以dt
dz/dt=∂z/∂u x du/dt +∂z/∂v x dv/dt
(2)多元套多元:
Z=f(u,v),u=(x,y), v=(x,y)
以求Zx偏导为例:
∂z/∂x=∂z∂u x ∂u∂x+∂z∂v x ∂v∂x
(3)全微分不变性
①条件:Z=f(u,v),u=(x,y), v=(x,y)
②结论:dz=∂z/∂x x dx+∂z∂y x dy =∂z/∂u x du+∂z∂v x dv
③证明:
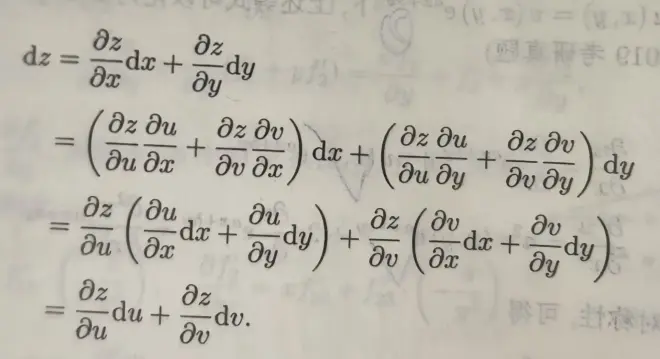
(4)变量相关型
①∂^2z/(∂y∂x)=【∂(∂z/∂y)】/∂x
②∂z/∂y=xcos(xy)+∂φ/∂y
③∂φ/∂y=φ1(x,x/y)dx/dy+φ2(x,x/y)d(x/y)/dy
=-φ2(x,x/y)x (y)^-2
这里φ1,φ2表示对位于第一项/第二项变量中的y求导
④∂z/∂y=xcos(xy)-φ2(x,x/y)x (y)^-2
⑤【∂(∂z/∂y)】/∂x=cos(xy)+xsin(xy)(-y)
-y^-2 φ2(x,x/y)-x/y^2 ∂φ2/∂x
⑥∂φ2/∂x=φ21(x,x/y)dx/dx+φ22(x,x/y)d(x/y)/dx
这里φ21中的1指的是对φ2这个函数的第一项中的x求导,φ22同理
⑦∴原式=cos(xy)-xysin(xy)-y^-2 φ2(x,x/y)
-x (y^-2) φ21(x,x/y)-x (y^-3) φ22(x,x/y)
⑧fx(x,x/y)与f1(x,x/y)(偏导x)的区别:
前者是对函数内所有x求偏导,后者是对第一项变量含有的x求偏导

