直线与圆公式、方法、二级结论全梳理，事半功倍！

直 线 与 圆

知识体系

直线部分

一.过定点

注意：直线只有一个参数时，很有可能过定点

①明问直线过哪个定点

②藏在条件里问

注意：垂直于x轴，则斜率接近于无穷大

二 . 斜率 K

①定义：代数

几何意义：斜率公式的几何意义很重要（出现类似结构，考虑斜率）

注意：直线斜率定义域左闭右开

遇见分式结构，想想能不能使用斜率的形式（即斜率公式的几何意义）

如下

②夹角公式

真的挺有用！

③性质

1.平行与垂直

直线与圆的题一定要注意暗处的隐藏条件

2.斜率互为相反数

这两条直线一定是关于平行于坐标轴的直线是对称的

④弦长公式（距离公式）（重要：很多圆锥曲线大题都会用到）

如何推出？（利用了三角函数）

弦长公式的作用：

1.能联系上K

2.比两点距离公式未知数少

三.其他距离公式（除弦长公式外）

点到直线

圆到直线（和点到直线本质相同）

所有圆到直线的距离，最终都转换为了点到直线的距离

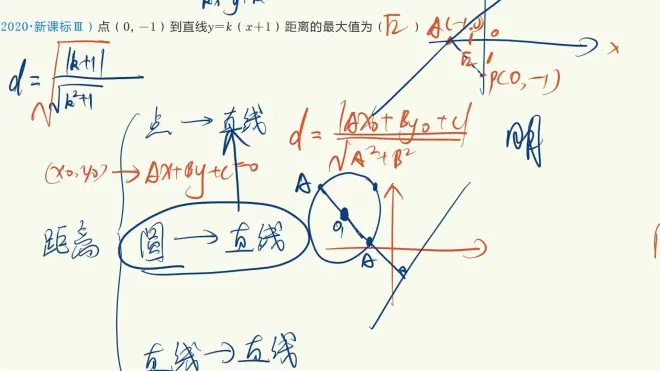
直线到直线

点到点（即两点间坐标公式）

如

四.对称性

①两点关于直线对称

②两圆关于直线对称

首先，圆心坐标根据上面点点关于直线对称求，之后利用半径相等

③两直线关于直线对称（对称轴一般平行于x轴或y轴）

（当对称轴是斜着的时候）

法一：首先利用 法二：

两点关于直线对称求得A' 求得交点

之后求得交点 之后利用对称轴上的点

再利用两点式 到两条直线距离相等求K

再利用点斜式

使用时哪种简单用那种

再复杂一些

圆的部分

一.方程

用一般式：题目告诉过哪几个点，让你写圆的方程

如下：尽量选有零（👻）的

研究圆心与半径时，用标准式

二.圆与圆之间位置关系（看d和r1，r2的关系）（不常考）

①相交（🍌）

注意：公共弦方程

②（👂）相切与相离（都比较简单）

三.直线与圆的关系（考的较多）

①位置关系

相切考的最多

②相切小点

公切线

求法 满足两个相切即可

注意：直线与圆一定要注意有没有隐藏条件

公切线求法，如下

③🌂用几何的思想解直线与圆

1.直线与圆相交

可利用垂径定理

2.圆上一点切线方程

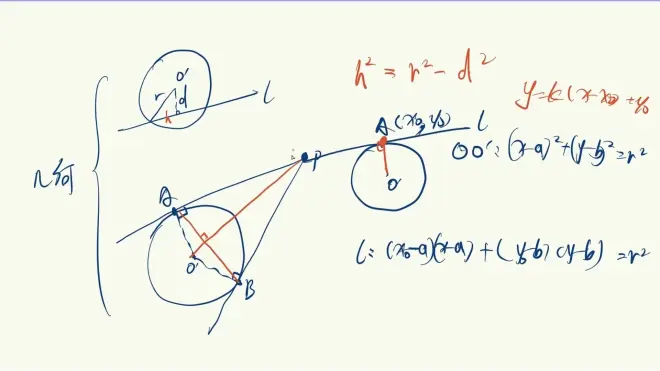
3.圆外一点切点弦方程

切点弦是 AB

也是上述方程

筝形：对角线乘积等于四边形面积的两倍

当发现题目中公式很难套的时候，就想想能不能利用几何性质（勾股，垂径定理，直角三角形等）