10.1 信息指纹：寓确定于随机之中

    计算机中的不同对象如果要存储下来不丢失任何信息，所需要的最少存储空间，就等于它们的信息熵，但如果只是区分，则远不需要这么长的编码，一种简单实用的做法就是用一种随机算法（通常是哈希算法），来将任何一段二进制信息映射成一个随机数，作为区别它和其他信息的指纹（fingerprint），当然这种伪随机数产生算法可能会产生概率很小的冲突或碰撞：

    考察当选取数字的总数量不断增加到很大时，不同信息产生相同信息指纹的概率不可忽视，此时信心指纹算法就不再适用了。采用逆向思维，考虑在什情况下不会出现重复的信息指纹。假定要随机挑选k个数，让它们不重复：第一个信息指纹可以有N中选法（N=2^128）；第二个N-1种，...，第k个指纹有N-k种，于是k个指纹不重复的概率：

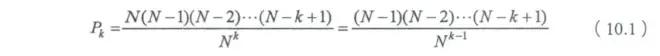
    由于Pk随k单调递减，来看一下Pk<=0.5时会发生什么，根据斯特林公式，当N非常大时：

    也就是说，对一个很大的N，k是一个很大的数，如果用MD5指纹验证，它有128位二进制数，算出来 k > 2^64 ≈ 1.8x10^19。即每1800亿亿次才能重复一次。

    信息指纹的【用途】有：

    1）网络爬虫需要知道每个网页是否已下载，记录URL要很多字节，直接存64位的信息指纹即可，大量降低存储压力

    2）比较两个文件是否相同，直接对比其信息指纹，因为随机性让不同目标无法映射到同一个数字上，带来了安全

    3）系统数据库或管理登陆的服务器中不再存储密码明文，而是只存密码的信息指纹（当然工业上还额外加盐（即随机数Salt））

10.2 随机性与量子通信

    这一小节很有意思，今天所说的量子通信，主要是利用光子的偏振特性传递一次性密钥，用一次性密钥对信息进行加密（香农Claude Shannon证明，只有一次性加密是完全无法破解的加密方式）

    发送端和接受段约定好两组信息编码方式（0，1的偏振光对应），然后在通信接收端放置偏振镜，就可以用来进行调制和解调：

    表10.1中，用+和x代表垂直/水平和45度/135度两种不同的调制方式，在调制时，随机采用上述两种方式，接收端由于不知道发送端是怎么做的，只能随便猜，假定接收方猜的结果如表10.2所示：

    在该例子中，6次一致，4次不一致，一致时接收端信息接收无误，但4次不一致时，接收信息可能有误，假定接收信息如表10.3所示：

    注意第4，6两个信息接收错误（【】中），第2，8两个（粗体数字）信息虽然偏振解调错了，但信息蒙对。一般，如果解调方式和调制一直，那么解码后信息误码率0%，这种情况占所有发送信息的50%左右；如果解调方式与调制不一致，解调后得到的信息也会有50%左右蒙对。即不论接收端如何设置偏振镜解调方向，最后得到的信息大约有50%x100%+50%x50%=75%和发送一致，误码率为25%。

    如果在传输过程中，信息被窃听截获，光子再经过被错误放置的光山时，偏振方向无从得知，得到0还是1完全随机，如果这时它再将信息转发给原本的接收端，接收端得到的信息只有75%x75%≈56%和发送端一致，如果接收端再将自己得到的信息送还给发送端确认，发送端就会发现只有56%的一致性，即可知道传输窃听，可以立即终止通信或采用其他信道。而中间窃听者运气好，得到信息和发送端一致性碰巧超过75%，而接收端得到的信息和它所转发的一致性也超过75%很多的可能性极小。比如发送1000比特时，窃听者经过一次转发仍有75%一致性的概率只有10^-35。

    当确定信道安全后，则需要确认双方通信密钥，发送端用明码将它所设置对的信息位告诉发送端即可。比如在例子中，第1、3、5、7、9、10位傻姑娘的信息，如表10.4:

    即便窃听者知道收发双方选用了第1、3、5、7、9、10位信息作为密钥，也不知道这些信息是什么。该协议被称作BB84，由其发明者Charles Bennett和Gilles Brassard在1984年发表。

10.3 置信度：成本与效果的平衡

    维特比算法（Viterbi Algorithm）的改进：该算法是一种特殊的动态规划算法，广泛应用于通信的解码问题，主要解决在图10.1所示的一种网格图中寻找最短路径：

        维特比算法针对这样一张图，从左到右一列列计算截止每一个时间点的最短路径，算法时间复杂度位O(K^2 * L)，如果想进一步改进维特比算法，需做近似，即需要剪枝：

    1）在计算完从七点到每一个时间点t的所有K条最短路径后，对它们做一次排序，放到优先队列Q中，从小到大排

    2）进行剪枝，假定队列Q中第一个路径长度为x，可以确定一个大雨1的常数c，把所有长度大于cx的路径都砍掉。当t大于某个阈值T之后，可以设定只保留m条路径（m << K），将计算复杂度降低到O(mKL)

    该算法也被称作聚光搜索（Beam Search）。其搜索工作原理示意如图10.2：

    由于一开始获得的前后相关信息较少，不确定性大，因此保留路径较多，但随着时间点的增加，即在网格图中走过的列的数量增加，获得了足够多的前后相关信息，可以开始大胆剪枝。此时短的那条路径和排在后面的路径之间的距离只差会不断增加，即如果一条候选路径没有排在前面，它以后拍到前面的可能性也不大，剪掉它们不影响最后结果。

    在聚光搜索中，最终的最短路径落在这m条候选路径中的概率和光束的宽度n有关，增加n可以提高该概率。通常在一个深度为几万的网格图中，把光束的宽度n限制在几十的范围内，已经能过保证99.9%甚至更高的置信度了。

总结：

    偶然性、随机性与确定性一样，也是这个世界的固有属性，有时候也要用偶然性来确定一个目标，判断真伪。当使用计算机解决问题时，通常会有一个理论上的最有算法，无法改进。但在实际应用中，我们依然有可能对某些特殊情况进行进一步优化，特别是在资源有限时，牺牲一些精确性，在一定的置信度下，获得对大部分情况下的有效处理。