角谷猜想是一个高阶逻辑问题

注意（10）式，是一个把全部过程放在一个公式里，无穷多个过程和未知数，是不可能一次性求解的。就是说，3x+1猜想无法证明。

3x+1 問題的运行模式。是一个由实践推出的命题，實踐只有上升到理論才能獲得理性認識。

公式是實踐的理論。公式化以后才能看清楚问题的结构与性质。角谷猜想就是说这种结构最后都是1.

（一），把問題公式化理論化

把角穀猜想規則用公式表示：3X+1.

通過下麵公式迭代，我們把 問題轉換成為一個迭代方程，也就納入了一個控制論的體系了，因為，只要有輸入，輸出，反饋.....等等，我們實際上已經進入了控制理論。

 

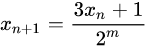
，.........（1）

這裏公式中每一個 x都是奇数。m=1，2，3，.....。 

.直到把 

 中的偶數析出抵消，使得（1）式右邊是奇數為止。

如果不是1而是其他奇數，就繼續迭代。一直到1為止。

最終使得（1）式等於1：

 

，....（2）

（二）舉例

例如 

,

代入公式： 

結束。

例如， 

 , 

 

, 

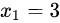
两步結束。

角穀是說，輸入 

 X=1，3，5，7，9，11，....任何一個奇數，直至無窮，經過（1）式迭代，都是（2）式等於1。

二，問題難倒了全世界的數學家

需要證明兩個結論以後才有可能完成：

1，任何一個 x值 進入迭代以後不會回到自身，就是不會發生循环。如果發生循环，表明是一個反例，否定了角穀猜想。

2，  進入迭代以後數值不會發散，就是不會越來越大直至無窮，而是在一個有限的範圍內更替。

倒行逆施

（一）， 把（1）式中的 

 

.......（3）

使得（3）式一步完成的 

 的 

 有：

,这时，

 

: 

 时，

=5， 21， 85， 341，1365， 5461， 21845， .....。因為這個 

是把（3）式反推的結果,：

 

........（4）。

例如： 

 =5， 

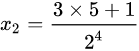
 ; 3x5+1=16= 2^4.

 .

=21, 

, 

 .;3x21+1=64= 2^6.

 .

 

 .因為3x85+1=256= 2^8

 .

這些 

 都是1。

.......。

（二），把（1）式两步完成的

  =1的公式：

 .....（5）

在（5）式二步到位 

 

=1的有：3, 13, 53, 113, 227, 909，.....。

 ......（6）

（6）式這個 

是把（5）式反推的結果。

例如：

代入公式（1）需要兩步：

； 

 

用（6）式即 

時。

用（5）式也可以： 

。

 

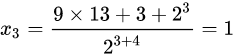
代入公式（1）需要兩步，

 ； 

 。

有（6）式 

 時。

用（5）式也是一樣 

......。

大家看，（6）式代入（5）式，剛好抵消。我們先把（6）式簡化：

,

，把（6）式右端代入（5）式：

我們可以一直進行下去，把（5）式擴展到任意n，對於任何 

： 

.....(7)

把（6）式擴展到任意n，對於任何一個奇數 

 ,

。..........(8)

把（7）式簡化：

........（9）。

把（8）式代入（7）式分子分母刚好抵消： 

 

.

.......（10）。

角谷猜想就是要证明：对于任何奇数都可以用（8）式表示。

例如， 

 

.......。

于是，人工智能就是设计好未来运行的规则，在没有人操作的情况下，完成预先的计划。

(10)式是一个倒装公式，好比一家几十代，几百代子孙在同时出现，这是无法求解的。陶哲轩是证明了这个猜想，这是不可能的。