高中数学基础与解法全集(涵盖所有)|长期更新|从零开始拯救所有学渣!通俗易懂|高

P161随机抽样
1.简单随机抽样
2.分层抽样
3.系统抽样(等距抽样)
P162 163分析样本
1.频率分布
1.极差
2.组数(5--9组)
3.组距
频率分布直方图:面积=频率
频率分布折线图:1.取长方形的中点,连线
2.将组距无限小
组数无限多
形成平滑曲线(总体密度线)
茎叶图:同时统计两组数据
2.数字特征
1.平均数
2.众数:最高柱的中点值
3.中数:使得面积等于1/2的点
4.标准差=√方差
(离散性,稳定性)
P164
百分位数

画轴(取两端结点),按比例求
P165
方差知识补充
∑(西格玛):求和符号
P166
1.随机试验
1.相同条件
可重复进行
2.结果明确
(正:硬币,非正即反)
不止一个(反:1+1=2)
3.恰好出现一个结果
不可事先确定结果
2.样本点(元素)
样本空间(集合)
1.随机事件[1,2]
基本事件(一个样本点)[1]
2.必然事件
3.不可能事件ø
有限样本空间
P167
事件的关系与运算


P168
古典概型
1.有限性(骰子1,2,3,4,5,6)
2.等可能性(骰子6个数字等可能)
3.P(A)=k/n=n(A)/n(Ω)
P169
概率的基本性质
1.随机事件A
P(A)≥0
2.必然事件
P(Ω)=1
不可能事件
P(Ø)=0
3. R,G互斥 (即RUG=ø)
P(RUG)=P(R)+P(G)
4.A,B对立(即A∩B=ø,AUB=Ω)
P(A)=1-P(B)
P(B)=1-P(A)
5.A⊆B,P(A)≤P(B)
6.

解题可参照 树状图
P170
事件的相互独立
P(AB)=P(A)P(B)
1.分类用+
甲中乙不 与 甲不乙中
2.分步用x
甲中 与 乙不
解题习惯:1.分类用{
2.分步用,

P171
频率和概率
频数足够大时,频率与概率相近
P153直线的斜率与倾斜角



P154
直线方程的四种表示
1.点斜式(前提:k存在)

2.斜截式(前提:k存在)
将(0,b)带入点斜式,可推的

3.截距式 (不能过原点)
两个点确定一个直线
带入(a,0)和(0,b)


4.两点式(已知两点)
由 点斜式 推得(将k代替)




P155
点,直线距离公式
1.公式
1.点与点
2.点与直线
3.直线与直线(相互平行的)
1.取一点,转化为点与直线
2.直线与直线公式


2.横过定点
一个含参直线(系数只有一个未知数)一定过定点:运用参数分离
(将参数提出,视未知数已知)
将 (1-2a)x+(3a+2)y-a=0
转化为 (-2x+3y-1)a+(x+2y)=0
P156
圆的两种方程表示
1.圆的标准式(由两点距离公式推得)
2.圆的一般式(配方后,与标准式雷同)
一般式 配方为 标准式


给三个点,多用一般式(消元)

求谁的轨迹,就设谁的坐标,找关系
标准方程中 x与y 的系数相等就是圆,但是求r时,将系数转为1

P157
1.直线和圆的位置关系
法1.比较d与r
(相切时,最佳方案)
d=圆心到直线的距离
r=半径
1.d>r相离
2.d=r相切
3.d<r相交
法2.看∆
圆的方程 与 直线方程 联立
(求交点坐标时,最佳方案)
1.∆>0相交
2.∆=0相切
3.∆<0相离
2.圆与圆的位置关系
d=圆心的距离
1.d>r1+r2相离
2.d=r1+r2外切
3.r1-r2<d<r1+r2相交
三角形中 两边和<第三边<两边差
4.d=r1-r2内切
5.d<r1-r2内含

P158
直线与圆 例题




P159
直线倾斜角 例题




P160
特殊直线性质:1.过定点(只含一个未知参数)


2.对称性(垂直平分)



P97
解三角形(一)
1.优先 角化边
2.tan若不能直接求,则化为sin/cos 3.sinacosb+ cosbsina=sin(a+b)
4.观察分母,注意通分
5.提取公因数
6.cos公式中a,b,c替换时,分母多不变(便于计算)








P98
解三角形(二)
思维
1.最值
2.变换
3.图形
措施
1.画图
2.若求角,但给边,则边变角
3.若求角,减少未知数(多角转单角)
4.先看 大的三角形,再看 小的
5.已知三边一角,用余弦定理(cos)
6.判断 三角形是否已经固定(唯一)
AAS,SAS,ASA,SSS
7.若求边 1.余弦定理
2.不等式
3.两边和,两边差







P172
椭圆的定义
P173
椭圆的习题课
1.m+n=2a(椭圆的第一性质)
2.a,b,c的关系(a最大)
3.e<1
4.长轴 短轴

P174
双曲线的定义
P175
双曲线的习题
1.m-n=2a(双曲线的第一性质)
2.a,b,c的关系(c最大)
3.e>1
4.与x轴的交点(a,0)
5.渐近线
6.实轴2a 虚轴2b
半实轴a 半虚轴b
7.求e(要a,b,c的两条方程)
已知一个隐藏关系(a,b,c),在题目中找另一个


1.
双曲线上的点到焦点距离的最小值

2.
思路

3.
计算策略

P176
抛物线的定义
P177
抛物线的习题
1.e=1
1.长度问题,BT=BF
2.横坐标关系,韦达定理
3.准线
4.准线的垂线
5.相似
6.中位线




P178
椭圆的第一定义与方程
(一个点 到 两个点的距离之和 为定值)

1.
找不变的量,不变的长度

2.
看定点(多为椭圆,双曲线)

3.
注意定义域

4.
极值点

P179
椭圆中的焦点三角形问题
1.2a
2.已知中点,画中位线
3.Rt∆勾股
4.一般三角形,用正余弦
1.
中点

2.
正弦余弦

3.
一般三角形,正弦余弦(边长比)

4.
先把未知数少的方程,化简

P180
点差法(设AB点坐标,方程做差)
已知(间接或直接)中点,中点弦问题,用点差法
推公式
公式沟通 斜率和中点
(公式中,a²是x底下的数,b²是y底下的数,无论大小)

1.

2.
m,n谁大不重要。公式中,a²是x底下的数,b²是y底下的数,无论大小

3.
先求中点,然后用点差法
列出公式,看公式差什么,就用条件求什么
注意定义域(如此题,y-1/x-0,x≠0,所以还要讨论x=0时)

P181
椭圆小题进阶(拔高)
1.几何性质
2.计算
1.点差法
2.未知就设,会约掉的
1.
内心:角平分线的交点
角平分线定理:角平分线两边比与两角对边比相等,作垂用相似就可以证明


2.看见共线,想斜率相等(多用 中间的点分别和另两点的斜率)


3.相似三角


4.


P182
双曲线方程求法(基础)
1.m-n=2a(第一定义)
2.渐近线

1.要检验c>a

2.

3.Rt∆勾股

4.
看渐近线,先求渐近线方程
列示:题目已知条件和隐藏条件(第一定律和abc关系)

5.看见中点,画中位线

6.角度问题(如平行),用正余弦(多用余弦),若不知边长,可构造三角形

计算

P184
抛物线的几何性质(中档)
1.设未知数(将所求量,用未知数表示)
添辅助线(准线的垂线)
2.先列出隐藏条件(图形特点)
3.再列题目给的(特有条件)
1.看抛物线,想抛物线的定义

2.作准线的垂线

3.作准线的垂线,将 所求量 用相同的未知数表示

基本不等式(四种形态)

P185
大题中的弦长公式(中档)
1.小题(第一问),列条件
2.大题,列大纲(所求量的表达式),然后依次求其中的未知数
证明


1.


2.
求面积
法1.
1/2*弦长*顶点到弦的距离


法2.
与x轴的交线长*(A到x轴的距离+B到x轴距离)

正式:y=kx+b
要分类讨论,直线是否 垂直x轴
反式:x=my+n
直线可能垂直x轴,且不可能平行x轴,设反式

联立(为了得到A,B坐标关系x1x2,y1y2)后,合成用y的方程,因为这样没有1/m(即1/k),直接用m(计算方便)


三个数的基本不等式公式


方程只含一个参数,一定过定点(求出M点坐标)
求MN,用点到直线距离公式

注意用不等式,要检验 是否可以取到 =号

P186
大题中的垂直翻译(基础)
垂直情况1.两个斜率可求 用k1*k2=-1
(重两直线本身)
(求单点坐标)
2.两个斜率联系小,不便求 用向量
(给一定点,重点信息集中在一条直线)
(求两点坐标关系,如x1x2)

1.
用向量(设点坐标) 翻译垂直

x用y代,因为若y用x代,则会有根号
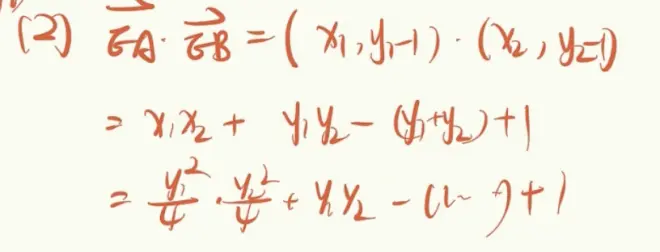

联立(两个未知点连成的直线 与 曲线 的联立),设反式
想得到关于x的式子,用正式
想得到关于y的式子,用反式

韦达定理 求y1y2的值

2.设斜率,因为三点中一点(中间的)已知,且只要求单点x值,不用求两点x1x2,y1y2关系


联立(一个未知点和已知点的直线 与 曲线 的联立 ),设正式,因为想求x的关系



