MATLAB进行聚类时确定簇数k的四种内部评估方法

聚类评估方法分为内部评估法和外部评估法。
内部评估法是指在没有外部标准的情况下,通过聚类结果本身的特征来评价聚类的质量。常见的内部评估方法有轮廓系数、DB指数等。
而外部评估法是指通过与已知的外部标准进行比较来评价聚类的质量,常用的方法有调整兰德指数(adjustedRand index,ARI)、标准化互信息法(Normalized Mutual Information,NMI)等。
在实际应用中,内部评估法比外部评估法要更加实用。因为内部评估法不需要外部标准,只需要根据聚类结果本身的特征来评价聚类的质量,而外部评估法需要已知的外部标准进行比较,有点类似于计算分类问题中的正确率、召回率等,但是需要有已知的标签,而这样的数据在聚类中非常少见。
下面我们介绍MATLAB支持的四种内部评估法,这四种方法可以帮助我们在聚类前确定聚类的克类别数K(有多少簇)的大小。
这四种方法的整体思想都大同小异,大家可以思考:一个好的聚类结果是什么样子?
一个好的聚类结果应该是不同类之间的差异尽量大,而同一类的样本尽可能的聚集。不过,不同的内部评估方法在计算聚类结果的质量时,会考虑到不同的因素,因此,不同的内部评估方法可以从不同角度评价聚类结果的质量。

下面我们介绍MATLAB中的四种内部评估法,这也是学界用的较多的几种方法:
https://ww2.mathworks.cn/help/stats/evalclusters.html
每个方法下方都有其被提出的参考文献。

(1)轮廓系数 Silhouette criterion
Rouseeuw, P. J. “Silhouettes: a graphical aid to the interpretation and validation of cluster analysis.” Journal of Computational and Applied Mathematics. Vol. 20, No. 1, 1987, pp. 53–65.
轮廓系数是一种聚类评估方法,它可以用来衡量聚类的质量。它的计算方式是计算样本与其所在簇中其他样本的距离和与其所在簇外其他簇中样本的距离和之差,然后将这个差值除以两者中的较大值。这个值越接近1,说明聚类效果越好;这个值越接近-1,说明聚类效果越差;这个值接近0,则说明聚类效果不明显。
MATLAB官网上有轮廓系数的介绍,但是不是很详细:
https://ww2.mathworks.cn/help/stats/clustering.evaluation.silhouetteevaluation.html

算法介绍来自MATLAB官网
注意最后一段话:ClusterPriors是轮廓系数计算时的一个参数,用于确定轮廓系数的计算方式。如果ClusterPriors的值为’empirical’,则软件通过对所有点的轮廓系数取平均值来计算聚类解的轮廓系数值。每个簇根据其大小成比例地贡献到准则值中。如果ClusterPriors的值为’equal’,则软件通过对每个簇内所有点的轮廓系数取平均值,然后在所有簇之间取平均值来计算聚类解的轮廓系数值。无论其大小如何,每个簇都对准则值做出相等的贡献。最优聚类数对应于具有最高轮廓准则值的解。在MATLAB中,ClusterPriors默认为’empirical’,和Python中sklearn包的计算方法是一致的。我们在使用时使用默认的选项即可。
下面是wiki上对于轮廓系数公式的推导,这里介绍的非常详细!

如果要使用轮廓系数确定聚类的类数k,只需要在不同的聚类数k分别计算轮廓系数即可。然后选择轮廓系数最大的那个k值。

(2)Calinski-Harabasz指数
Calinski-Harabasz指数,由Calinski和Harabasz在1974年提出:
我们希望SSB(簇间方差)尽量大,即不同的类之间的差异尽量大;
SSW(簇内方差)尽量小,即同一类的样本尽可能的聚集!
Calinski, T., and J. Harabasz. “A dendrite method for cluster analysis.” Communications in Statistics. Vol. 3, No. 1, 1974, pp. 1–27.

https://ww2.mathworks.cn/help/stats/clustering.evaluation.calinskiharabaszevaluation.html
英文水平不好的同学可以看下面这篇文章:

因此,从公式可以看出,Calinski-Harabasz指数越大、说明聚类效果越好。
(注意,在SSB和SSW一定的情况下,聚类的数目k和Calinski-Harabasz呈反比关系,而在实际聚类过程中,随着k的增大,SSB会变大、SSW会变小,因此这里面有一种权衡取舍关系!这也是为什么要添加k-1和N-k的原因)
如果要使用Calinski-Harabasz指数确定聚类的类数k,只需要在不同的聚类数k分别计算Calinski-Harabasz指数即可。然后选择Calinski-Harabasz指数最大的那个k值。

(3)Davies-Bouldin指数
Davies-Bouldin指数,由Davies和Bouldin在1979年提出:
Davies, D. L., and D. W. Bouldin. “A Cluster Separation Measure.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. PAMI-1, No. 2, 1979, pp. 224–227.
Davies-Bouldin指数的核心思想是计算每个簇与它的最相似簇之间的相似度,然后再通过求得所有的相似度的平均值来衡量整个聚类结果的优劣,而这个相似度是基于簇之间的距离刻画的!
如果簇与簇之间的相似度越高(此时Davies-Bouldin指数偏高),也就说明簇与簇之间的距离越小(直观上理解只有相距越近的事物才会越相似),那么此时聚类结果就越差,反之亦然。
因此,Davies-Bouldin指数越低,说明聚类效果越好。
相关的计算公式可参考MATLAB官网:

算法介绍来自MATLAB官网
https://ww2.mathworks.cn/help/stats/clustering.evaluation.daviesbouldinevaluation.html
知乎上有篇文章写的也很好:
https://zhuanlan.zhihu.com/p/530944459
以下截图来自这篇文章:


如果要使用Davies-Bouldin指数确定聚类的类数k,只需要在不同的聚类数k分别计算Davies-Bouldin指数即可。然后选择Davies-Bouldin指数最低的那个k值。

(4)间隙统计量(Gap criterion clustering evaluation)
这个方法在2001年由斯坦福大学的三位学者提出,发表在统计学领域理论推导类级别最高的期刊上。根据Google Scholar数据显示,截至2023年3月,该论文已经被引用了超过6300次,引用次数非常多。这表明该论文对聚类分析领域产生了重要的影响,并且被广泛应用于实际问题中。
算法的原理和前面三个方法相比是最难的,感兴趣的同学可以搜索下面的论文:
Tibshirani, R., G. Walther, and T. Hastie. “Estimating the number of clusters in a data set via the gap statistic.” Journal of the Royal Statistical Society: Series B. Vol. 63, Part 2, 2001, pp. 411–423.
该方法提出了一个新的统计量,名为:Gap statistic(间隙统计量)。
通过计算不同聚类数K对应的Gap statistic,来确定最佳聚类数。
Gap statistic可以衡量当前聚类数的聚类效果与原始数据集具有相同的分布特征的随机数据集的聚类效果之间的差距。具体来说,Gap statistic是由ExpectedLogW和LogW两个值的差异得出的,其中ExpectedLogW是由Monte Carlo方法得到的期望值,而LogW是当前聚类数下的对数似然值。
计算过程如下:

公式里面的W_k是原始数据集中k个聚类簇的簇内距离之和(求和之前分别除以了两倍的簇内样本量)。

有两种方法生成与原始数据集具有相同的分布特征的随机数据集:

第一种方法基于均匀分布生成,计算简单但可能不能很好的刻画原始分布的特征;第二种方法基于主成分分析的思想,能考虑到数据分布的形状,是一种自适应的分布,这种自适应分布计算更加复杂但能更准确地反映原始数据集的特征,因此更推荐使用。
注意,该指标不是越大越好,也不是越小越好,如果要使用Davies-Bouldin指数确定聚类的类数k,最佳的簇是满足下面的规则的最小的k:

上式中,B就是随机数据集的样本个数,论文中的例子将B设置为100。然而,在实际应用中,B的具体取值可能会因数据集大小、聚类数目、计算资源等因素而有所不同。一般来说,如果计算资源允许,可以将B设置得更大以提高估计的准确性。但是需要注意的是,当B过大时可能会导致计算时间过长。 因此,在实际应用中,我们可以根据具体情况来选择合适的B值。如果数据集较小,则可以将B设置为100是足够的;如果数据集较大或者需要更高的估计精度,则可以将B设置得更大。
在我自己写的聚类工具箱中,我将B设置成一个和样本量有关的数值,当样本量小于200时,B等于100,当样本量大于等于200时,B等于样本量的一半。
MATLAB官网也有该方法的介绍,具体可参考:
https://ww2.mathworks.cn/help/stats/clustering.evaluation.gapevaluation.html

MATLAB官网的这段介绍将k的选取和肘部法则联系了起来,事实上使用间隙统计量选择k的过程和使用肘部图确定k的方法有点像(肘部图随着k的变大是单调递减的,间隙统计量随着k的变大通常会先上升),只不过肘部图中的k是我们肉眼观看确定的,而间隙统计量的最佳的k是可以通过计算确定的。
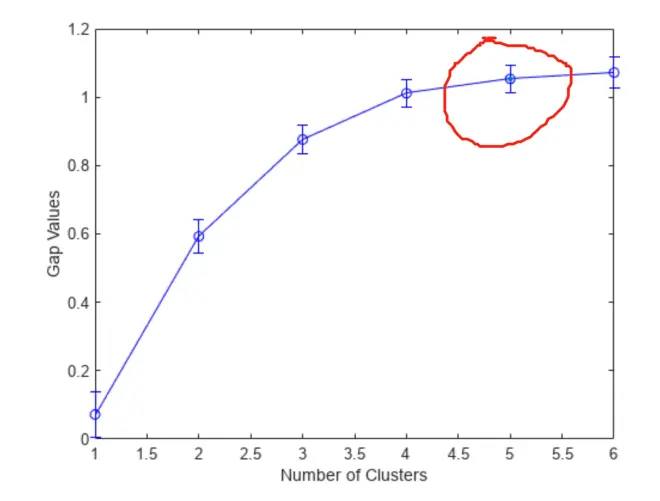
下图来自MATLAB官网:使用鸢尾花数据集确定最佳聚类数,得到的结果是分成5类。
附上正课第十讲上肘部法则的介绍:



