平面向量坐标与建系教学！题目无系，心中有戏

这里是官方认证的优秀科代表渡鸦~看看这黄闪电。今天带来平面向量建系法的有关内容。包含例题分析与重点总结。绝对不只是简单截图哦

Part 1：向量坐标的基本知识

这部分知识比较基础，相信老师应该都讲了，这里就不过多赘述了。稍微重要一点的是夹角的公式，通过用数量积除以模长乘积得到夹角。

看看基本运算的例题。

“无脑带公式就好了”——一鸽

向量中遇到夹角，一般都翻译为余弦值处理。表示出向量c，然后代入夹角的公式，解方程就好。需要注意的是，这里C的模长不用急着算，到时候可以消掉。

Part 2：几何与建系

先看看基本的例题。

（听说这是北京压轴，这么简单的吗）

给出直角肯定要按直角边建系的。 PC长度恒定，轨迹肯定是圆。这里考虑用三角函数可以简化计算。但如果直接硬设坐标也可以解。然后就是带公式硬算咯，别告诉我你连辅助角都忘啦。

再看一道稍微有点难度的。

为什么选择D点建系？是因为AED三点共线。这样可以简化A和E的坐标表达难度。然后还是带公式看有没有解。以及为了简化计算，我们直接设长度是1。

结论一并不只有2分之根号2一种解，但它是最简单的一个。

在看看图长得花里胡哨，但是难度其实不大的。

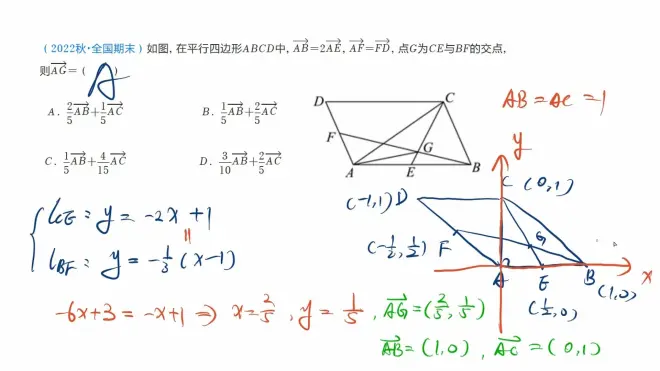
像这种没有很多限制条件的，建系时我们让它越特殊越好。怎样才算特殊？这一题要用基底AB、AC表示，而最特殊的基底莫过于垂直的单位向量。于是我们尝试让AB和AC垂直且长度等于1进行计算。

由于我们的基底是相互垂直的，我们只要求出G的坐标，就可以直接表示。这时就是初中几何的求直线交点了。

Part 3：代数问题建系

重点还是翻译条件。给出余弦，因为这题没有无脑的公式可代，所以换成夹角画一下图。然后等于0的条件，这里是直接设出了坐标，算出是轨迹是圆。|b-c|就是由c的末端指向b的末端，也就是CB。画出圆后就变成了一个初中的最短长度问题。

Part 4：总结

如果你的运算能力够好，向量确实全部都可以做。但很多时候，几何法更为简洁。为了日后着想，少建系，多几何~