【人工智能导论】实验二 一阶逻辑归结算法

以下是up主人工智能实验课的实验报告,写完顺手发到b站上留个档(当然如果能帮助到有需要的人更好,不过我估计也没有人会看的啦)有问题可以在评论区留言,虽然我也很有可能不会。

一、 实验题目
一阶逻辑归结原理实验
二、 实验内容
1. 算法原理
(1)子句归结
子句归结的理论原理是,假设有两个子句(其中C_1,C_2是子句,P是文字):

从中消去互补对(即和 ),所得的新子句

称作子句的归结子句,原子称为被归结的原子,这个过程称为归结。只有存在互补对的子句才存在归结式。对两子句做归结的过程即为求归结式。
在本次实验中,输入的要处理的子式为已经经过转换之后的便于计算机处理的Clausal form,即每一个子句对应一个元组,元组每一个元素是一个原子公式/原子公式的否定,元素之间的关系是析取关系,表示只要一个原子成立,该子句成立;元组的集合组成子句集S,子句集中每个句子之间是合取关系,表示每一个子句都应该被满足。
以上面三条式子为例,

对应的Clausal Form为

但是Clausal Form只是易于计算机进行处理的形式,并不是真正要用的形式,在程序中如果要对子句执行归结算法,(以Python为例)还需要将其转换成列表的形式。每个原子公式转换成一个以字符串为元素的列表,列表组成为[“谓词”, “项1”, “项2”, ……, “项n”],以上面的三个式子为例,转换之后真正进行处理的形式为:

如果是对不含变量的子句进行单步归结,主要过程为先检测两个要进行的列表是否为谓词相反、项数目相等的原子公式,然后再对除谓词外的所有项(即列表中除了第0个元素外的所有元素)进行对比,如果一样,则进行单步归结。
单步归结的算法的具体思想是:先标记两个子句中的互补对的位置,然后对两个子句进行深复制以后讲互补对删除,最后再将删除互补对之后的两条子句进行合并生成新的子句。注意在这个过程中可能出现两条子句中存在相同的原子公式,在加入子句集的之前要对生成的新子句去重。(即将重复出现的原子公式删除)去重在本程序中的实现方法是先转换成集合形式,再转变回列表。
(2)子句合一
当两个子句中存在变量时,如果可以通过变量替换使得两个子句能被归结(具有相同的原子),则将变量替换成常量使得两个子句归结的过程叫作合一。合一也被定义为使得两个原子公式等价的一组变量替换/赋值。
例如,如果两个子句为

则可以将第二个子句中的变量y替换为A,此时两个子句就有相反谓词的原子公式,这时再进行归结的操作,生成新的子句。
两个子句合一后生成的新子句为

在程序当中,合一的操作同样以Clausal From的形式进行处理的。程序中进行合一操作的基本思想是:
①首先判断要进行合一的两个子句中是否存在变量并且长度相同,然后进入函数judge中,judge输入两个要进行判段的子句并且返回一个列表或者false。
②在judge中,从项(即从下标为1)开始同步遍历两个子句,如果两个子句中的项是常量则相等,并且继续遍历下一个项;如果一个子句中为变量,而第二个子句中为常量,则将这两个项记录到要返回的列表中。并且继续下一个循环;如果遇到其他情况则直接返回false。最后当所有项都遍历完并且没有返回false的情况下返回记录了替换项与被替换项的列表。
③judge结束后,判断judge的返回值,如果返回值为false则不能进行合一。如果返回值为列表则依据列表中记录的项对两个子句进行合一操作,主要的操作是将互补对消去,并且将含变量子句中的其他相同变量改为被替换的常量,最后再进行归结操作。生成的新子句加入到子句集合中。
(3)遍历子句集合
因为程序的输入不是单独的两个子句,而是多个子句,要保证所有的子句都能被判断一遍是否能进行归结和合一。所以设置一个四重循环,第一重循环遍历第i个子句;第二个循环遍历第j个子句;第三重循环遍历第i个子句的第ki个原子公式;第四重循环遍历第j个子句出现的第kj个原子公式。这样就能将每个子句的每个原子公式判断一遍。循环体内的内容就是前面的(1)和(2),即进行判断是否能归结、合一并加入新子句的操作。当生成空的子句时,就表示输入的子句集和可以被归结,此时直接退出循环。
(4)回溯有用子句并输出
成功生成空子句之后,就代表着输入的子句集合可以被归结,但是需要注意的是,此时子句集合中所生成的子句并不是所有的子句都是用的上的,因为在上一阶段即遍历集合生成空句的过程中,所做的操作是把所有能进行归结合一的子句进行归结,并加入到子句集合中。这时很多生成的子句就是无用子句(即在生成空子句的过程中用不上这些子句)。
而为了能找到正确的有用子句,此时就要从生成的空子句出发,回溯找到生成这个空子句所要用到的子句,并记录且输出出来。为了实现这一操作,还需要新增两个列表,分别是记录父归结子句的parent列表和记录变量、常量的assigment列表,这两个列表和子句集合S同步更新。
以最终生成的空子句为结点,可以得到类似下图的二叉树:

要回溯有用子句,就是对上面这个二叉树进行层序遍历,即我们可以将回溯子句的过程视为层序遍历二叉树的过程。
所以只需要以parent为索引,以队列为数据结构,对上图的二叉树进行层序遍历:创建一个新列表用来存储有用子句,首先将“根节点”空子句入队,将新入队的子句加入列表,同时将对应编号的parent和Assignment列表中的元素记录;然后查询它的父子句,再将其父子句入队、记录,当查询到原始输入的子句时(子句编号小于n)则不入队。往复循环,直到队列为空。
需要注意的是,此时记录的子式编号是原编号,即在子句集合S中的编号(包含了很多无用子句的编号)。这时就需要对已经记录的有用子句进行重新标号,以保证输出时能对应上是哪两个子句。比如最终生成的空子句原标号是S[42],重新标号后为S[10]。
最后再对已经记录的子句转换为Clausal Form再逆序输出即可。
2. 伪代码
(1)归结生成子句阶段
第一层循环以i为下标遍历所有子式:
第二层循环以j为下标遍历所有子式:
第三层循环遍历第i个子式的所有原子公式:
第四层循环遍历第j个子式的所有原子公式:
if 存在原子及其的否定(如On和它的否定¬On):
if可以直接进行归结:
进行归结操作;
将互补对消去生成新子句加入到子句集合S中;
记录变量替换情况assignment及其parents (i, ki, j, kj);
If 生成的新子句为空:
结束所有循环;
Else 判断是否可以进行合一:
If 不可以进行合一:
Continue;
Else 可以进行合一:
对要进行变量替换的那条子句中的变量替换为对应的常量;
消去互补对并将变量替换后的两个子句进行归结;
并将新生成的子句加入到子句集合S中;
记录变量替换情况assignment及其parents (i, ki, j, kj);
If 新生成的子句为空:
结束所有循环
第四层循环结束
第三层循环结束
第二层循环结束
第一层循环结束
(2)回溯寻找有用子句的阶段
创建队列q;
将空子句的parent入队;
记录空子句以及其变量替换情况assignment及其parents (i, ki, j, kj);
While 队列不为空:
记录队首子句;
出队;
If 当前子句的第一个父子句的标号大于n:
记录子句以及其变量替换情况assignment及其parents (i, ki, j, kj);
将第一个父子句的parent入队;
If 第二个父子句的标号大于n:
记录子句以及其变量替换情况assignment及其parents (i, ki, j, kj);
将第二个父子句的parent入队;
End While
3.关键代码展示
(1)读入初始子句集合

(2)遍历进行合一、归结
生成新子句函数:
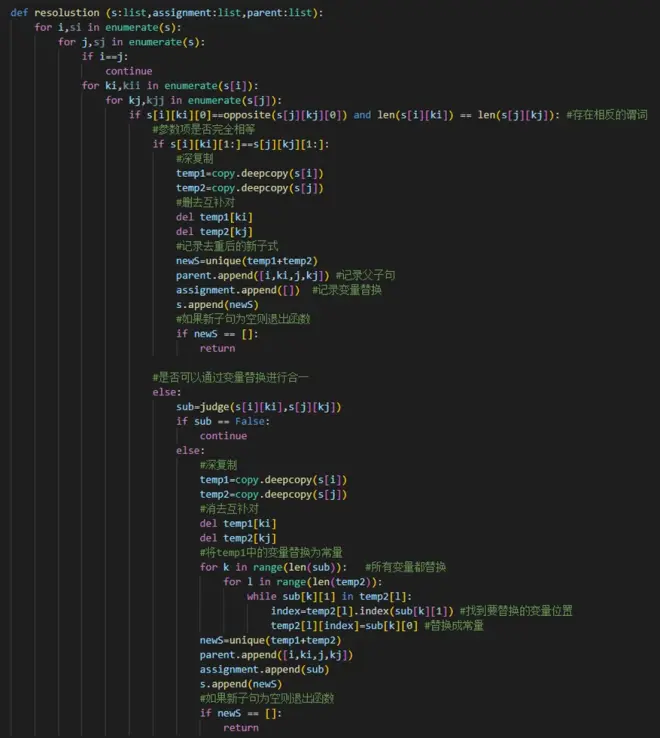
转换函数:

去重函数:

用来判断是否能进行合一并返回Assignment的judge函数:

(4)回溯寻找有用子句:

(5)重新标号:

(6)转换为标准形式再输出:

三、实验结果及分析
1. 实验结果展示示例
本程序采用的输入输出方式是在命令行窗口直接输入,并在命令行窗口即时输出。输入格式是首先输入原始子句的数目,然后再按行输入子句。
①Aipine Club

②Graduate Student

2. 评测指标展示及分析
本次实验的程序主要的时间复杂度集中在遍历子句进行归结以及合一这一阶段上,按照大O表示法的规则,整体程序的时间复杂度可以近似认为就是这一阶段的时间复杂度。
这一阶段的主要函数为resolution,函数利用了四重循环对,每个子句的每个原子公式都进行了一遍对比。这个函数的时间复杂度主要取决于输入的列表s的长度n以及每个子句的原子公式的数量m。
①当每个子句的原子公式数量比较少(只有个位数)的情况下(即本次实验给出的三个例子),程序的时间复杂度可以近似认为为 ;
②当子句的原子公式个数较多的情况下,考虑到进行合一操作时还要利用judge函数对两个子句的原子公式进行遍历,而这个操作的时间复杂度为,所以程序的时间复杂度为。(一般来说比这个要更大,因为程序内部还有利用循环替换变量等其他操作)
四、参考资料
[1]Lab2_归结原理课件
[2]人工智能(第三版),清华大学出版社

