欧拉公式与正多面体

  正多面体我们非常熟悉，比如一些结晶体就是特殊的多面体，它们的每个面都是全等的正多  面形，由此我们得到正多边形的定义:

             每个面都全等，且每个立体角都全等的多边体就是正多面体

   

   补充:如下就是以A为顶点的立体角

    欧拉公式

令E为多面体的棱数，V表示顶点数，F表示面数，则有以下式子成立：

                                              E=V+F-2

证明：若只有一个面，则

若有两个面，则

若有三个面（如下图）

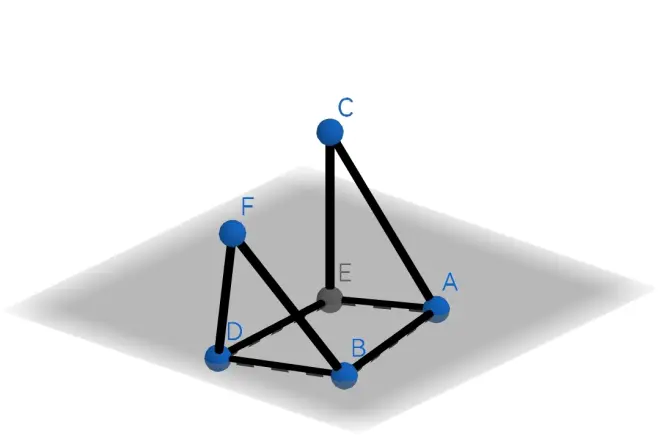
此时，必有2条或3条棱4个顶点重合,因此，增加的棱数比顶点数多1。故下式成立：

当填加第F个面时，面的棱和顶点都会与其他的面重合；故：

正多面体只有5个？是的，这个问题看似很简单，只要用顶点度数合小于360。（这里存在不严谨的地方，即用一种多边形到底可以得到几种多面体）但是这里给出另一种答案

设多面体每个面边数为m，F个面有mF条棱，则

设多面体每个顶点上的多面角有n条棱，V个顶点有nV条棱，则

带入欧拉公式，得

由于多面角的面角合为小于360，若用正三角形拼则只有三，四，五面角

所以，当m=3时,若n=3，E=6,F=4

n=4,E=12,F=8

n=5,E=30,F=20

当用的面为正方形时，m=4,n=3得E=12,F=6

当用的面为正五边形时，m=5,n=3得E=30,F=12

分析上面的数据后，我们可以只有5个正多面体了，其实这是很有趣的，不是吗？