机器学习——交叉熵

    首先先来说一下信息量f（x）这个概念的理解，一个不确定的概率事件X1，经过信息处理后，得到了一个确定的事件X2，相当于是一个不确定的事件发生了，变成了一个确定的事件，在这个过程中不确定事件X1的概率P越小，整个过程的信息量就越大，满足负相关的关系。如果X2由相互独立的随机事件X3 和 X4共同发生所确定，同时发生满足概率相乘，但信息量是相加的关系 f（X2）= f（X3 * X4） =f（X3）+ f (X4） 符合对数函数的定义。

    这个也就很好的得到了信息量的定义等式，f（X）是一个时间发生所能带来的信息量，x表示不确定性事件X的发生概率，以2为底的对数是为了对应比特位，多少个比特能表示这个事件发生的信息量。

    信息熵是针对一个系统而言的，一个系统中包含m个事件，每个事件发生的概率pi乘以该事件对应的信息量，所有事件叠加之后就是整个系统对应的信息熵，熵越大，系统中的不确定性越高，系统的混乱性也就越大。如果系统中每个事件发生的概率都相等的时候，此时最难预测发生的结果，整体混乱程度最大，信息熵最大。

    以系统P为标准，对于同一个事件i在Q中的信息量（i事件在Q系统中的概率）减去在P中对应的信息量（i事件在系统P中的概率），乘以在系统P中发生的概率pi，这个就是KL散度，衡量比较两个模型的差异大小，根据吉布斯不等式可知，信息熵（KL散度）恒大于0，在两个系统完全相同时取得等号。

    对于KL散度中后半部分是系统P的信息熵，在标准系统P确定之后就是一个确定的值，散度的大小由前半部分来确定，前半部分也被称为交叉熵。

    以二分类问题来讨论交叉熵在实际损失值中的运用，以下例子中使用猫猫分类问题进行讨论，输出结果yi是一个概率，1-yi就是不是猫的概率，是由模型给出判断其有多大的概率是猫，xi就是真实情况图像是否为猫，概率值为0/1.

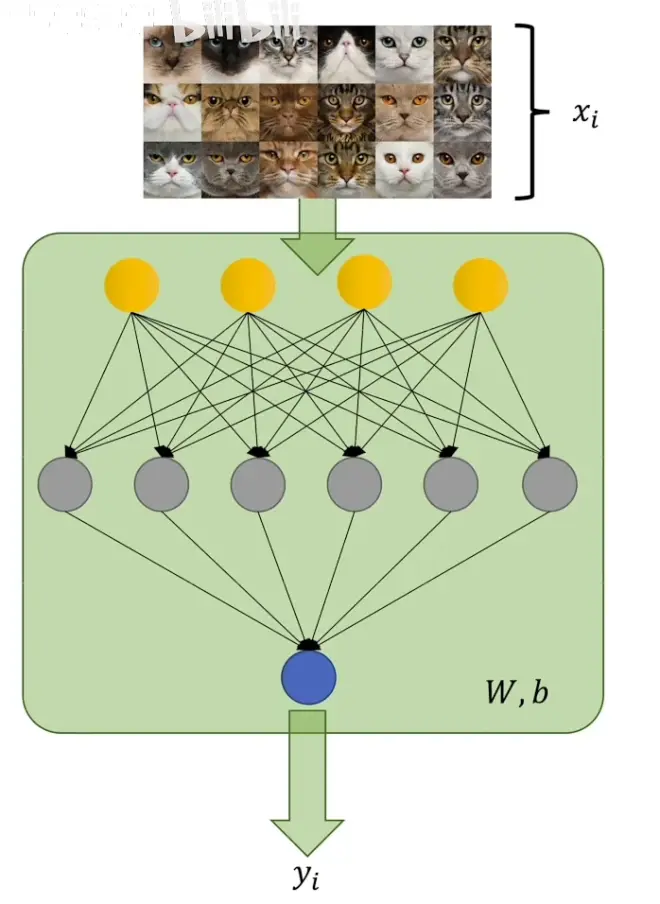
    在二分类问题中 ， i等于0/1，只有两种情况，叠加的符号就省略了，计算得到的损失值即可带入到反向传播的过程中进行运算。

    进一步来解释以下xi和yi的概率代表的实际含义。

    xi是人脑认为是猫的概率，是在基准P系统中的发生概率，也就是预计应该发生的概率。

    yi是模型认为是猫的概率，对应的是Q系统，相当于是在真实环境下采样得到的概率值。

    这个交叉熵的式子，也就是由模型预测事件的发生所带来的交叉熵。